Display Title
Math Example--Quadratics--Conic Sections: Example 9
Display Title
Math Example--Quadratics--Conic Sections: Example 9
Conic Sections: Example 9
Topic
Quadratics
Description
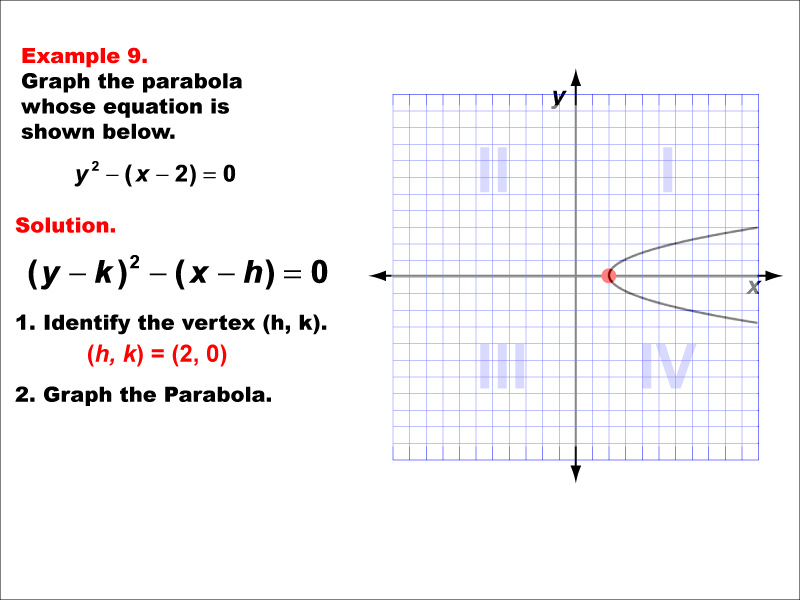
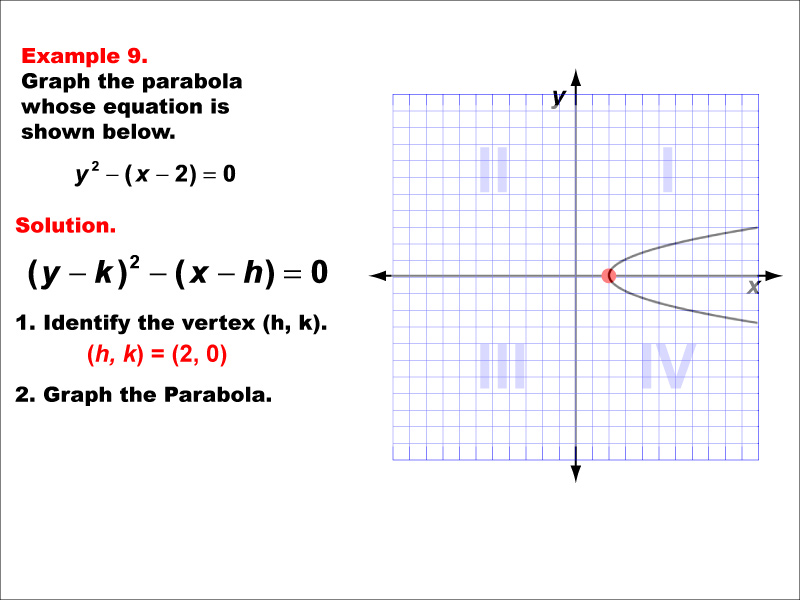
This example illustrates another horizontal parabola, but opening to the left. Its equation form is x = -a(y - k)² + h, where (h, k) is the vertex and 'a' is positive. The vertex is at (2, 0). Like all horizontal parabolas, this is not a function. This example highlights the versatility of conic sections in representing various shapes and orientations. Understanding these variations is crucial in fields like calculus (optimization problems) and physics (optics). Conic sections provide a foundation for modeling real-world phenomena and solving complex problems in science and engineering.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |