Display Title
Math Example--Quadratics--Equations of Parabolas--Example 9
Display Title
Math Example--Quadratics--Equations of Parabolas--Example 9
Equations of Parabolas--Example 9
Topic
Quadratics
Description
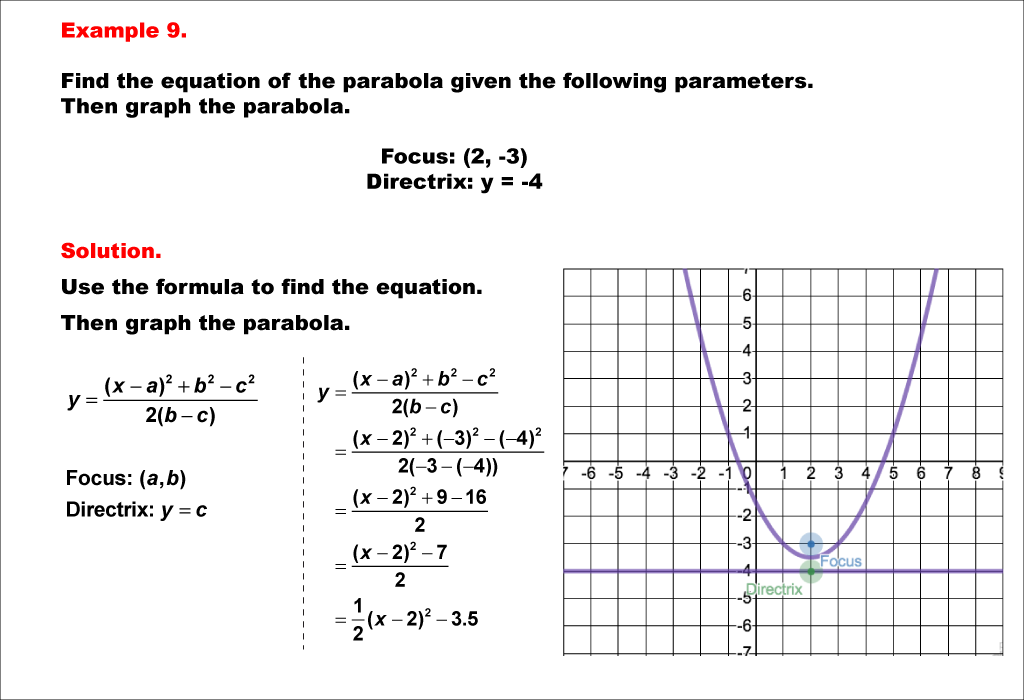
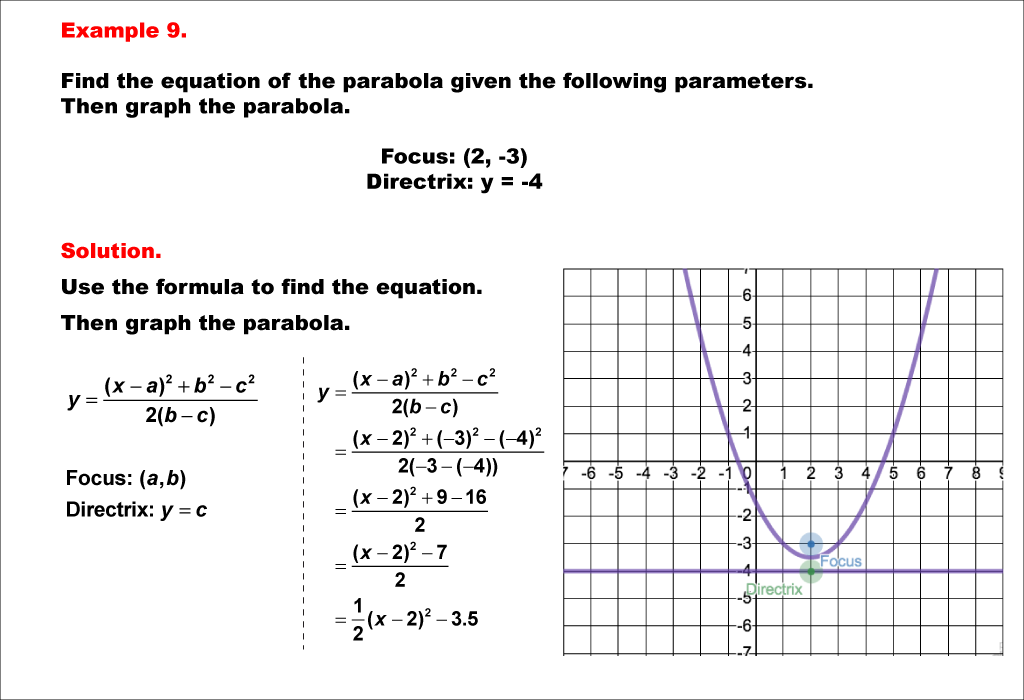
This example shows a parabola with its focus at (2, -3) and directrix y = -4. The vertex is at (2, -3.5), and the parabola opens upward. The distance p from the vertex to the focus is -4. The directrix is a line perpendicular to the axis of symmetry and is located at a distance |p| from the vertex on the opposite side of the focus. The axis of symmetry is a line that passes through the vertex and the focus, dividing the parabola into two symmetric halves.A parabola can also be defined as the locus of points in a plane that are equidistant from a fixed point (the focus) and a fixed line (the directrix).
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.A, CCSS.MATH.CONTENT.HSG.GPE.A.2 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Graphs of Quadratic Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, focus, directrix |