Display Title
Math Example--Quadratics--Parabola Axis of Symmetry: Example 2
Display Title
Parabola Axis of Symmetry: Example 2
Topic
Quadratics
Description
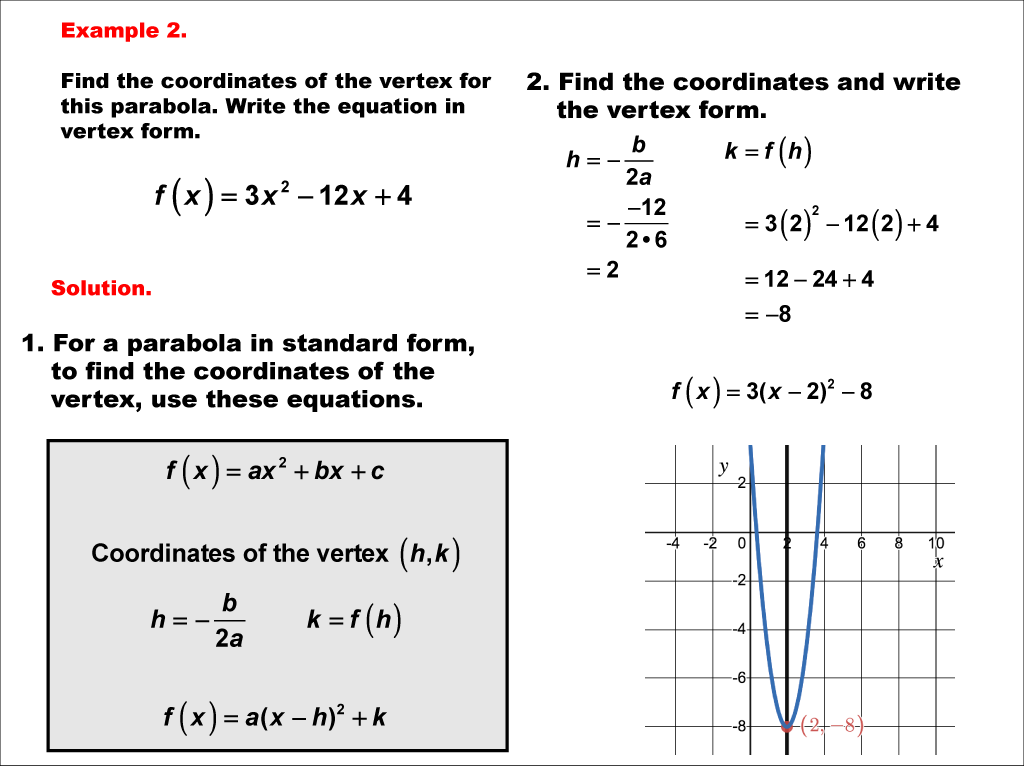
The axis of symmetry is a vertical line that passes through the vertex of a parabola, dividing it into two mirror-image halves. For a quadratic function in the form f(x) = ax² + bx + c, the axis of symmetry can be calculated using the formula x = -b / (2a), where a and b are the coefficients of the quadratic equation.
This example presents the quadratic function f(x) = 3x² - 12x + 4. To find the axis of symmetry, we apply the formula x = -b / (2a). Here, a = 3 and b = -12. Plugging these values into the formula, we get x = 2. This vertical line bisects the parabola, creating a mirror image on either side. This can also be used to find the vertex form of the parabola.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Graphs of Quadratic Functions • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | parabolas, axis of symmetry |