
Display Title
Math Example--Quadratics--Parabola Axis of Symmetry: Example 5
Display Title
Parabola Axis of Symmetry: Example 5
Topic
Quadratics
Description
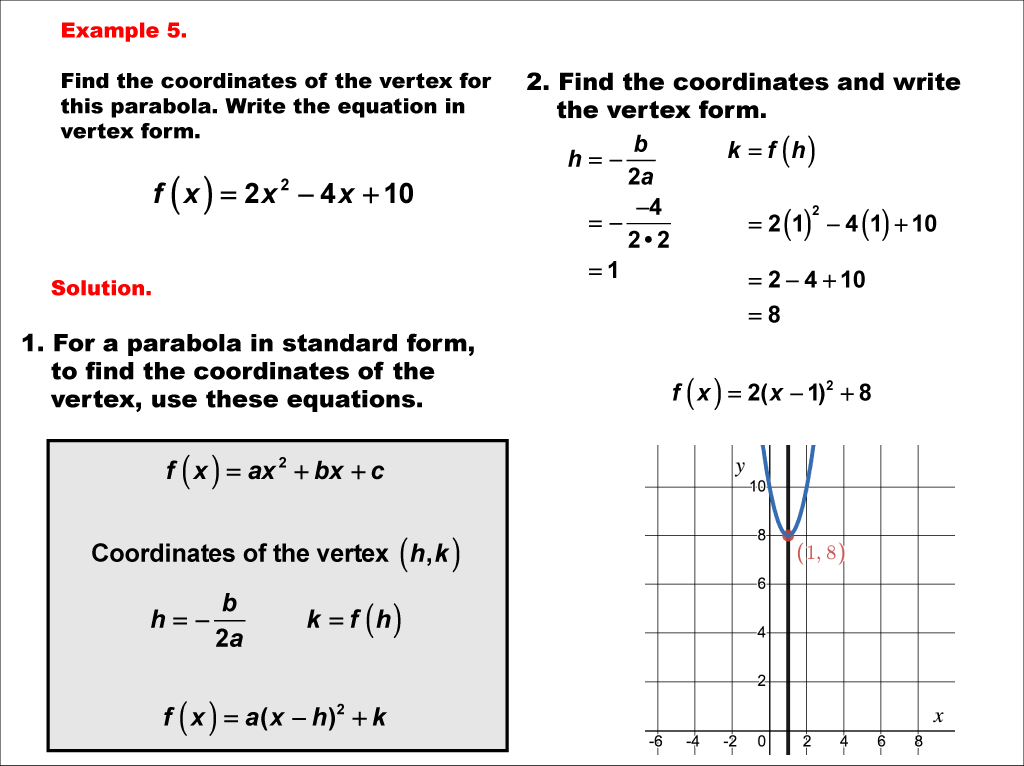
The axis of symmetry is a vertical line that passes through the vertex of a parabola, dividing it into two mirror-image halves. For a quadratic function in the form f(x) = ax² + bx + c, the axis of symmetry can be calculated using the formula x = -b / (2a), where 'a' and 'b' are the coefficients of the quadratic equation.
In this example, we're given the quadratic function f(x) = 2x² - 4x + 10. To determine the axis of symmetry, we use x = -b / (2a). Here, a = 2 and b = -4. Calculating, we get x = 1. The axis of symmetry is x = 1. This line passes through the vertex of the parabola, which is the minimum point since the parabola opens upward (a is positive).
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Graphs of Quadratic Functions • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | parabolas, axis of symmetry |