Display Title
Math Example--Quadratics--Solving Quadratics by Completing the Square--Example 6
Display Title
Solving Quadratics by Completing the Square--Example 6
Topic
Quadratics
Description
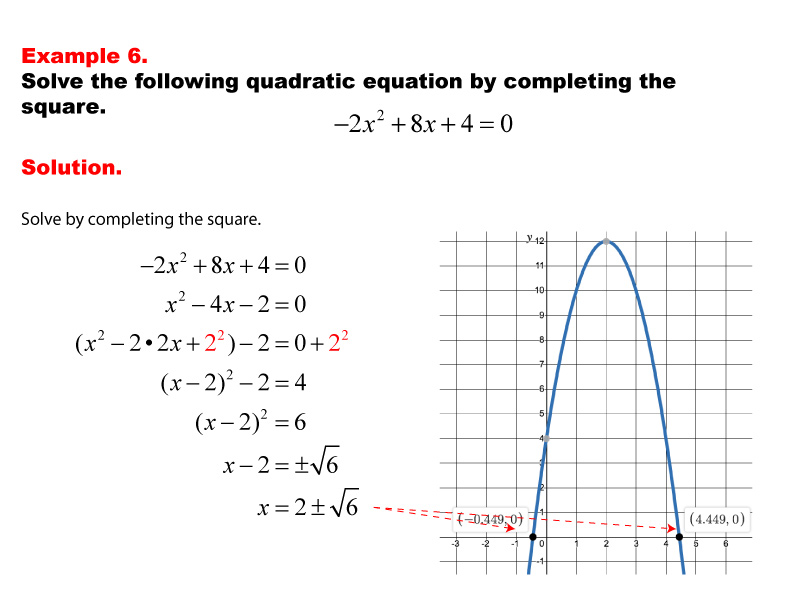
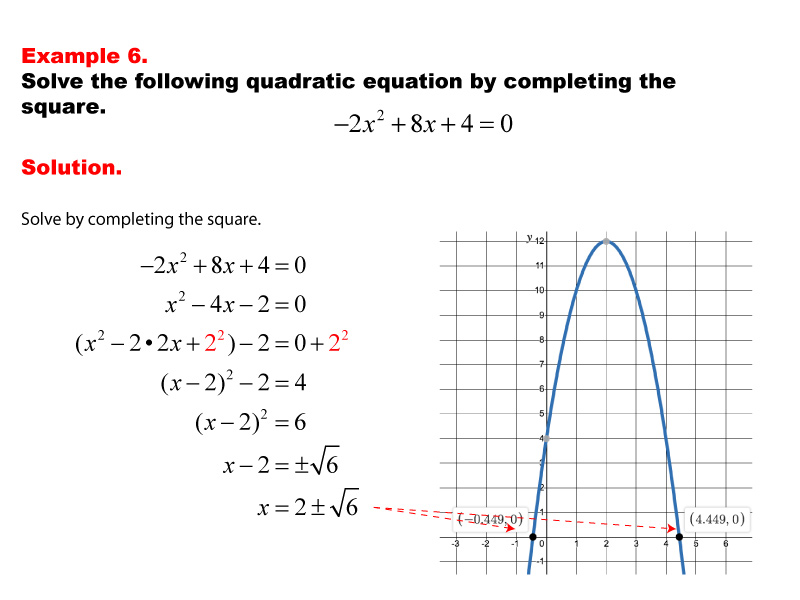
This example demonstrates solving a quadratic equation by completing the square. The equation is manipulated to form a perfect square trinomial, simplifying the process of finding the roots. The graphic shows each step of the technique, highlighting its utility in solving quadratic equations through symbolic manipulation and providing a clear path to the solution.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
Solving Quadratic Equations
Quadratic equations are usually written as a quadratic expression in standard form equal to zero.
A quadratic equation can have two, one, or zero real number solutions. There are several ways to solve a quadratic. These are the methods we’ll be looking at:
- The Quadratic Formula
- Factoring
- Graphing the Quadratic Function
- Completing the Square
Let’s look at the first method, which will work for any quadratic equation.
The Quadratic Formula
When a quadratic equation is written in standard form, like the one shown below, then you can use the quadratic formula to find the solutions to the equation.
Use the a, b, and c values from the quadratic equation and plug them into the quadratic formula:
To learn more about using the quadratic formula to solve quadratic equations, click on this link. This slide show includes a video overview of the quadratic formula and a number of detailed math examples.
Before using the quadratic formula, calculate the discriminant, which is the term under the square root sign of the quadratic formula.
To see examples of using the discriminant, click on this link.
Factoring
You’ve already seen how to factor quadratic expressions into the product of linear terms. That same idea can be used to factor certain quadratic expressions in order to find the solutions to the equation.
A factored quadratic equation will look something like this:
The solutions to this equation are x = a and x = b.
A more simplified version of a factored quadratic can look like this:
The solutions to this equation are x = 0 and x = a.
The previous two examples both had two solutions. There is a factored form that has one solution:
This is the case of the binomial squared. In this case the solution to the equation is x = a.
The simplest example of the binomial squared is this:
The solution to this is x = 0.
If a quadratic cannot be easily factored, then you should use the quadratic formula or graph the quadratic.
To see examples of using factoring to solve a quadratic equation, click on this link.
Solving by Graphing
A visual approach to solving quadratic equations is to graph the parabola. There are three cases to look at.
Case 1: Two solutions. If the graph of the parabola intersects the x-axis twice, then there are two solutions.
Suppose you are solving this quadratic equation:
To find the solution graphically, then graph the corresponding quadratic function.
Notice that this parabola intersects the x-axis at x = 2 and x = 4. Those are the solutions to the quadratic equation. In fact, you can rewrite the quadratic in factored form:
Case 2: One solution. If the graph of the parabola intersects the x-axis once, then there is only one real number solution.
Suppose you are solving this quadratic equation:
To find the solution graphically, then graph the corresponding quadratic function.
Notice that this parabola intersects the x-axis at x = -2. This is the solution to the quadratic equation. In fact, you can rewrite the quadratic as a binomial squared:
Case 3: No real solutions. If the graph of the parabola doesn’t intersect the x-axis, then there are no real solutions to the quadratic equation.
Suppose you are solving this quadratic equation:
To find the solution graphically, then graph the corresponding quadratic function.
Notice that this parabola doesn’t intersect the x-axis. When this happens, the quadratic equation doesn’t have real number solutions. It does, however, have complex number solutions, which you can find using the quadratic formula.
Summary of Solving by Graphing. When a parabola intersects the x-axis, then the parabola has at least one real number solution. These intersection points are also referred to as:
- x-intercepts
- Zeros of the Quadratic Function
- Roots of the Quadratic Equation
To learn more about solving a quadratic equation graphically, click on the following link. This includes a video tutorial and several worked-out math examples.
Solving Quadratic Equations Example 1 The parabola with the equation shown below intersects the line with equation y = 16 at two points, A and B. What is the length of segment AB? For a question of this type, where references are made to graphs and intersection points, it’s best to draw a diagram to get a better understanding of the problem. The equation shown is of a parabola in vertex form that intersects y = 16. Sketch that. We know the y coordinates for A and B; in both cases it’s 16. To find the corresponding x-coordinates, solve this equation: The x-coordinate for point A is x = 4 and the for B it’s x = 12. So the distance from A to B is the difference, or 8. Example 2 In the quadratic equation below, a is a nonzero constant. The vertex of the parabola has coordinates (c, d). Which of the following is equal to d? When a quadratic is written in standard form, the vertex has these coordinates: Write the function in standard form. Now find the corresponding x and y coordinates with this equation. Example 3 The parabola whose equation is shown below intersects the graph of y = x at (0, 0) and (a, a). What is the value of a? To get a better understanding of this problem, draw a diagram. To find the value of a, solve the following equation: |
How to Complete the Square
This way of solving a quadratic involves rewriting the quadratic equation in standard form and rewriting it in a way to find the roots using a square term. Let’s look at an example.
This is a quadratic equation in standard form. To use the technique of completing the square, take the two x-terms and place them in parentheses.
The goal is to take the expression in parentheses and write it as an expanded square term. Recall that a linear term squared has this type of expansion.
So, if we want to take the previous expression and rewrite it as an expanded, it would look like this:
What value goes in the box to make this a squared expression? The number is 4. Do you see it?
This is what the squared term looks like.
Let’s go back to the original quadratic equation.
All we need to do is add a 42 to the term in parentheses. But we can’t just add this value without subtracting that same value. Otherwise, the equation would no longer be true. So this is how to write the equation.
Notice that the term 42 is added to the expression in parentheses but also subtracted outside the parentheses. This keeps the original equation intact, but now you have a square term in parentheses. You can rewrite the equation this way.
Now it’s in a form where you can isolate the variable to solve for x. Follow these steps.
The solution is identical to what you would get had you used the quadratic formula. But with some quadratic equations, completing the square provides a useful alternative.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.B.4.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2020 |
| Keywords | quadratic equations |