Display Title
Math Example--Rational Concepts--Graphs of Rational Functions: Example 1
Display Title
Math Example--Rational Concepts--Graphs of Rational Functions: Example 1
Topic
Rational Functions
Description
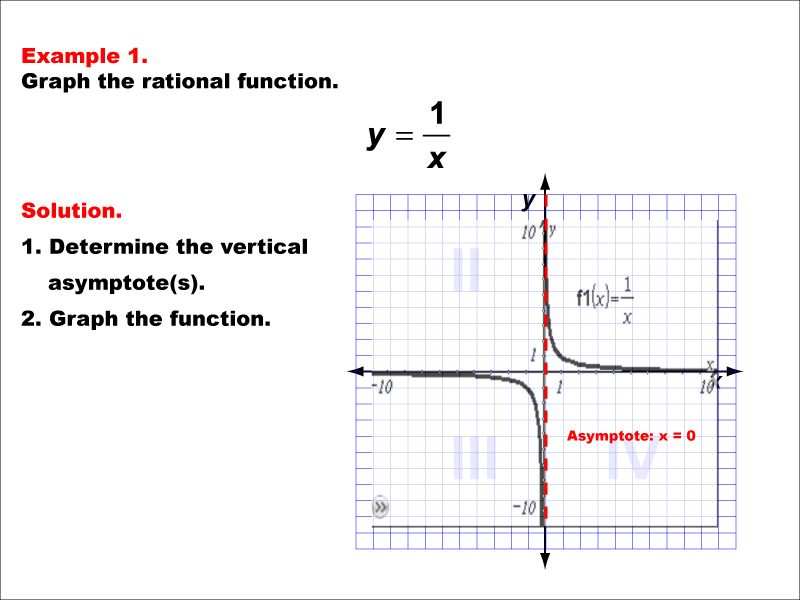
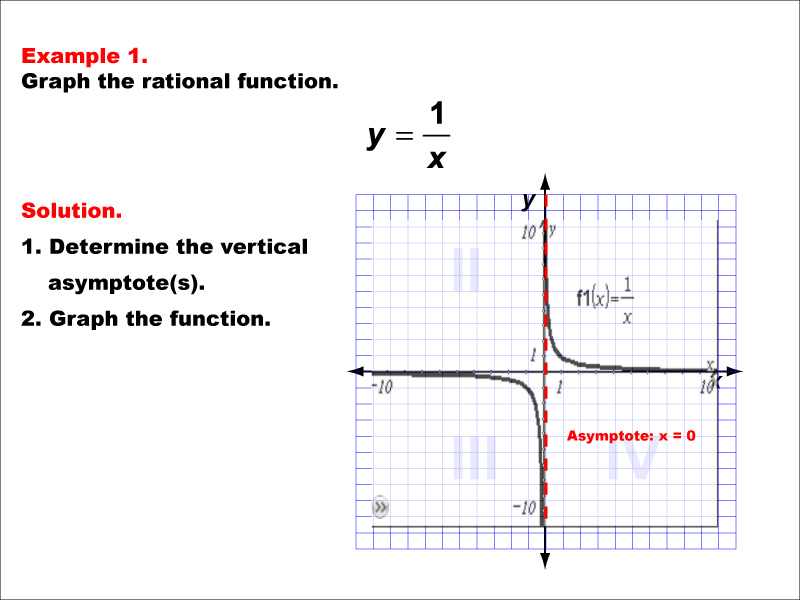
This example demonstrates the graph of the rational function y = 1 / x. The graph is a hyperbola with vertical and horizontal asymptotes, with the vertical asymptote occurring at x = 0. Students are tasked with graphing the function and determining its vertical asymptote.
Rational functions are a crucial topic in algebra, involving fractions of polynomials. This collection of examples helps teach the topic by providing visual representations of various rational functions, allowing students to observe how changes in the function affect its graph. By examining multiple examples, students can identify patterns and develop a deeper understanding of asymptotes and function behavior.
Exposure to multiple worked-out examples is essential for students to fully grasp mathematical concepts. It allows them to see different scenarios, reinforces key ideas, and helps build problem-solving skills. This repetitive exposure can boost confidence and enhance overall comprehension of rational functions.
Teacher's Script
Let's examine the graph of y = 1 / x. Notice how the function approaches infinity as x gets closer to zero from both sides. This behavior defines our vertical asymptote. Pay attention to how the graph never actually touches the y-axis or x-axis, instead approaching these lines as x or y values become very large or very small. Understanding these characteristics is key to mastering rational functions.
For a complete collection of math examples related to Rational Functions click on this link: Math Examples: Graphs of Rational Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2013 |
| Keywords | functions, rational functions |