Display Title
Math Example--Rational Concepts--Graphs of Rational Functions: Example 5
Display Title
Math Example--Rational Concepts--Graphs of Rational Functions: Example 5
Topic
Rational Functions
Description
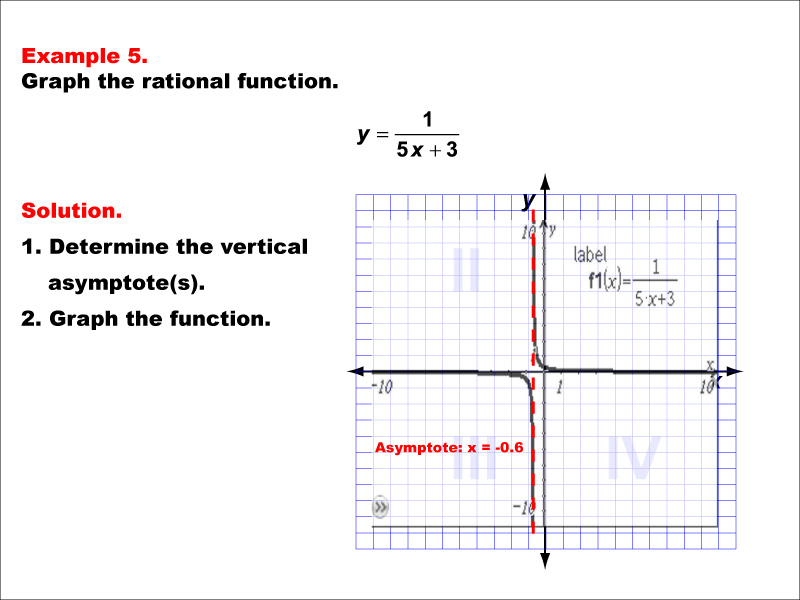
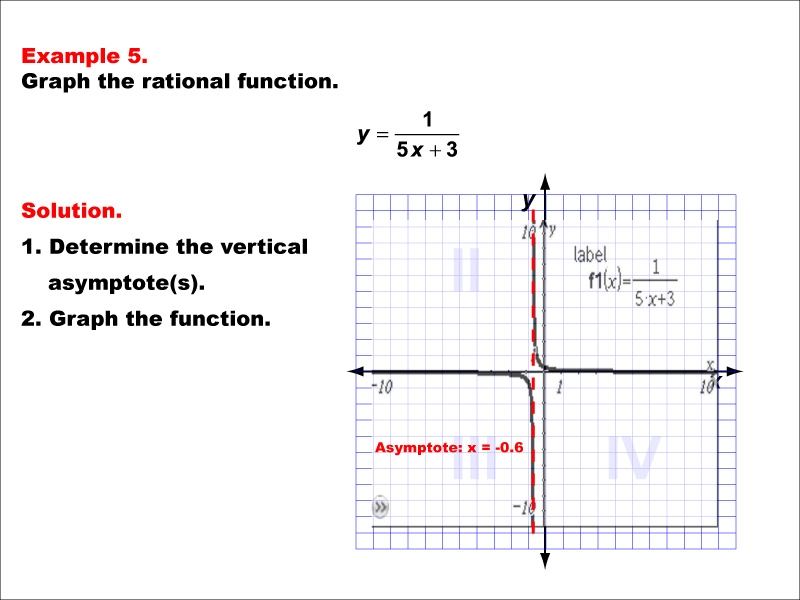
This example illustrates the graph of the rational function y = 1 / (5x + 3). The graph features a vertical asymptote at x = -0.6, indicated by a dashed red line. Students are tasked with graphing the function and determining its vertical asymptote.
Rational functions are a fundamental topic in algebra, involving fractions of polynomial functions. This collection of examples facilitates teaching the topic by providing visual representations of various rational functions, enabling students to observe how changes in the function affect its graph. By studying multiple examples, students can identify patterns and develop a deeper understanding of asymptotes and function behavior.
Exposure to multiple worked-out examples is essential for students to fully grasp mathematical concepts. It allows them to encounter different scenarios, reinforces key ideas, and helps develop problem-solving skills. This repetitive exposure can boost confidence and enhance overall comprehension of rational functions.
Teacher's Script
In this example, notice that the vertical asymptote is at a non-integer value, x = -0.6. This is because the equation for the asymptote is 5x + 3 = 0, which solves to x = -3/5 or -0.6. Observe how the function approaches infinity as x approaches -0.6 from both sides. Understanding how to determine the asymptote from the equation and visualize its effect on the graph is crucial for mastering rational functions.
For a complete collection of math examples related to Rational Functions click on this link: Math Examples: Graphs of Rational Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2013 |
| Keywords | functions, rational functions |