Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19
Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19
Topic
Rational Functions
Description
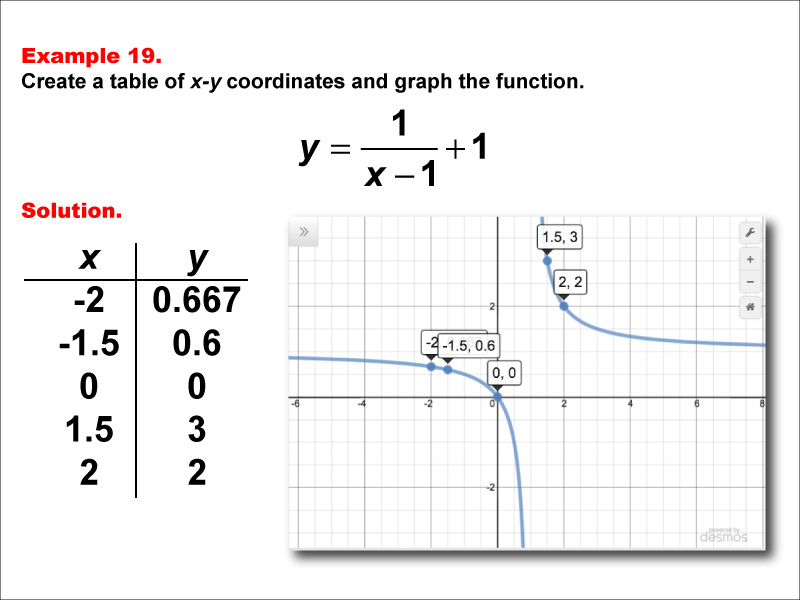
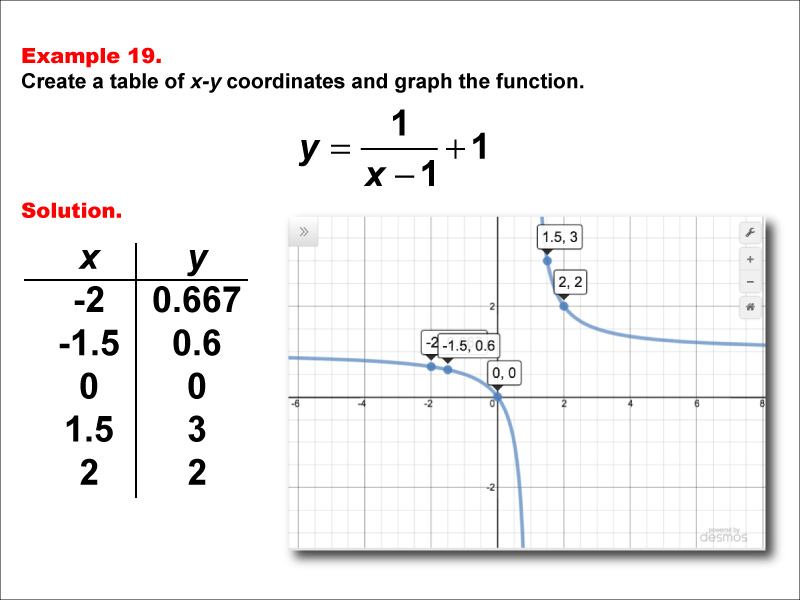
This math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x - 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. Points include (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is a hyperbola with asymptotes at x = 1 and y = 1, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position.
Rational functions are a crucial topic in algebra and calculus, representing the ratio of two polynomial functions with additional transformations. This collection of examples helps teach this topic by providing visual representations of various rational functions, allowing students to see how changes in the function affect its graph. By examining multiple examples, students can identify patterns and develop a deeper understanding of how constants in different parts of the function shift the graph both horizontally and vertically.
Seeing multiple worked-out examples is essential for students to fully grasp the concept of rational functions and their transformations. Each example builds upon the previous ones, introducing combinations of changes in the function that result in different graph shapes and positions. This approach helps students develop pattern recognition skills and enhances their ability to predict the behavior of rational functions based on their equations.
Teacher's Script: Let's examine our nineteenth example: y = 1 / (x - 1) + 1. How does this function compare to our previous examples? Notice that we've subtracted 1 in the denominator and added 1 to the entire fraction. What effect do you think these changes will have on the graph? As you observe the graph, can you explain why the asymptotes are at x = 1 and y = 1? How does this graph compare to y = 1 / (x + 1) + 1? As we continue with more examples, pay attention to how combinations of constants in different parts of the function affect the position and shape of the graph.
For a complete collection of math examples related to Rational Functions click on this link: Math Examples: Rational Functions in Tables and Graphs Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, rational functions, graphs of rational functions, rational function tables |