Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 28
Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 28
Topic
Rational Functions
Description
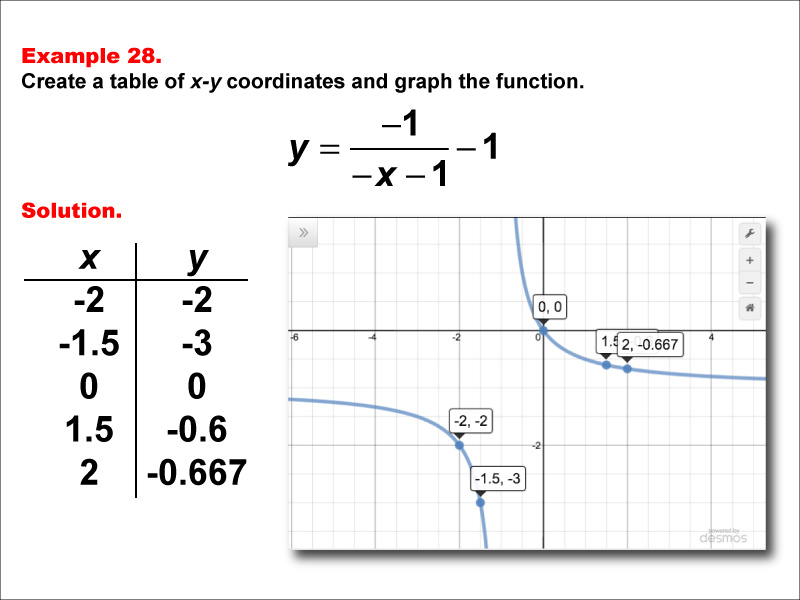
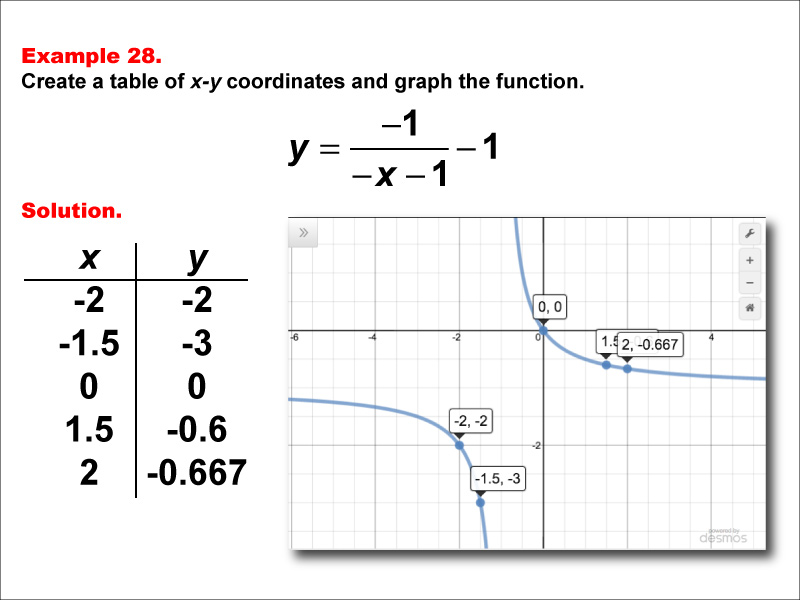
This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), and (2, -0.667), illustrating how negating both the numerator and the terms inside the parentheses, while subtracting a constant from the entire fraction, affects the graph's shape and position.
Rational functions are an important concept in algebra and calculus, representing the ratio of two polynomial functions with additional transformations. This collection of examples aids in teaching this topic by providing visual representations of various rational functions, allowing students to observe how alterations in the function impact its graph. By studying multiple examples, students can identify patterns and develop a comprehensive understanding of how negations and constants in different parts of the function shift, reflect, and transform the graph.
The importance of presenting multiple worked-out examples cannot be overstated when it comes to students fully grasping the concept of rational functions and their transformations. Each example builds upon the previous ones, introducing slight variations in the function that result in different graph shapes and positions. This approach enhances students' pattern recognition skills and improves their ability to predict the behavior of rational functions based on their equations.
Teacher's Script: Now, let's analyze our final example: y = -1 / (-x - 1) - 1. How does this function compare to our previous examples? Notice that we've negated both the numerator and the terms inside the parentheses, and we're subtracting 1 from the entire fraction. What effect do you think these changes will have on the graph? As you observe the graph, can you explain why it's positioned and shaped the way it is? How does it compare to y = 1 / (x + 1) - 1? As we conclude our exploration of rational functions, reflect on how the various combinations of negations and constants we've seen affect the graphs. Can you now predict how a rational function will behave based on its equation?
For a complete collection of math examples related to Rational Functions click on this link: Math Examples: Rational Functions in Tables and Graphs Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, rational functions, graphs of rational functions, rational function tables |