Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 4
Display Title
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 4
Topic
Rational Functions
Description
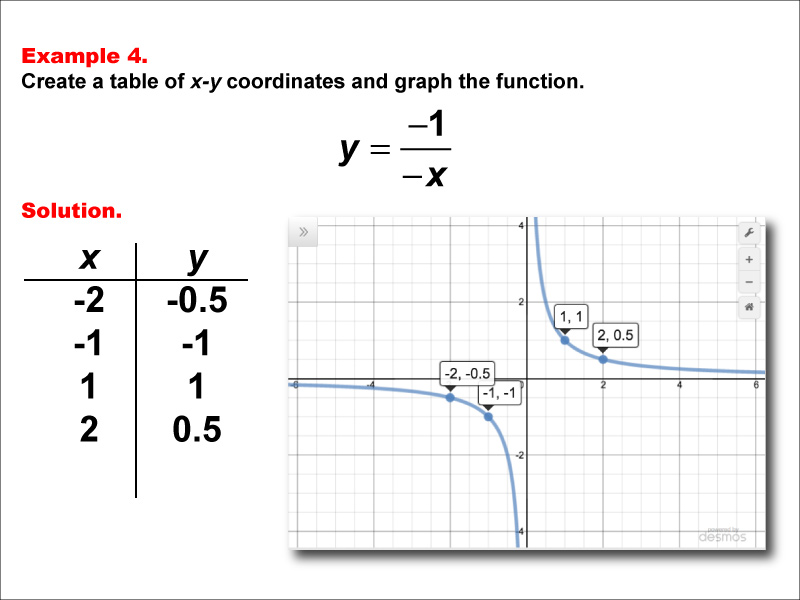
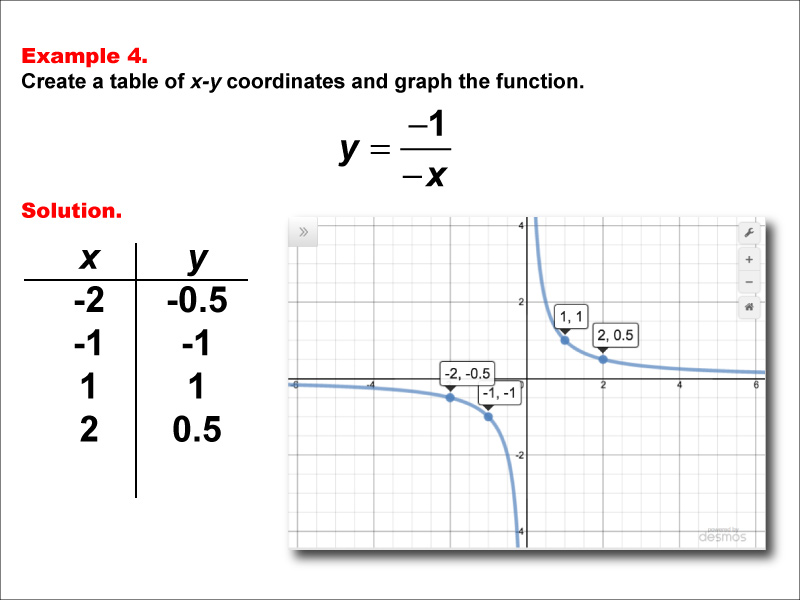
This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x). The image showcases both the table of x-y coordinates and the resulting graph. Notably, the graph is identical to that of y = 1 / x, displaying a hyperbola with branches in the first and third quadrants. This example further illustrates how different forms of rational functions can produce the same graph.
Rational functions are a key concept in algebra and calculus, representing the ratio of two polynomial functions. This collection of examples aids in teaching this topic by providing visual representations of various rational functions, allowing students to observe how different forms of equations can result in similar graphs. By studying multiple examples, students can identify patterns and develop a comprehensive understanding of rational functions' behavior and equivalence.
The importance of presenting multiple worked-out examples cannot be overstated when it comes to students fully grasping the concept of rational functions. Each example builds upon the previous ones, introducing different forms of equations that may result in similar or different graph shapes and characteristics. This approach enhances students' analytical skills and improves their ability to recognize equivalent forms of rational functions and predict their graphical representations.
Teacher's Script: Now, let's look at our fourth example: y = -1 / (-x). How do you think this graph will compare to our previous examples? When we plot it, we see that it's identical to y = 1 / x from our first example. Can you explain why this happens? What does this tell us about the effect of negative signs in the numerator and denominator of a rational function? As we continue exploring more examples, try to predict how different combinations of negative signs will affect the graphs.
For a complete collection of math examples related to Rational Functions click on this link: Math Examples: Rational Functions in Tables and Graphs Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, rational functions, graphs of rational functions, rational function tables |