Display Title
Math Example--Right Triangles-- Example 1
Display Title
Math Example--Right Triangles-- Example 1
Topic
Right Triangles
Description
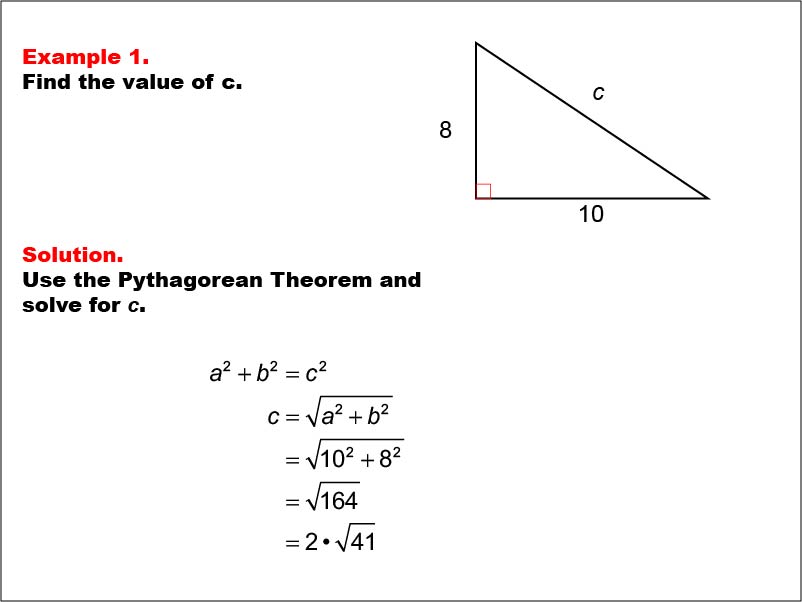
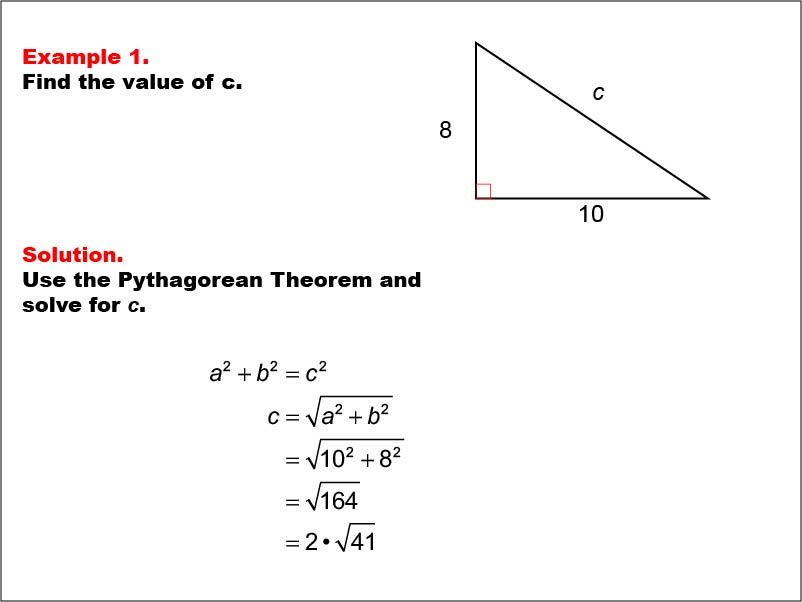
This example presents a right triangle with sides of length 8 and 10, and an unknown hypotenuse labeled c. The task is to find the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(102 + 82) = √(164) = 2 * √(41).
Right triangles are fundamental in geometry and trigonometry. They possess a unique property where the square of the hypotenuse (the longest side) is equal to the sum of squares of the other two sides. This property, known as the Pythagorean Theorem, is crucial for solving various problems involving right triangles.
Providing multiple worked-out examples is essential for students to fully grasp the concept of right triangles and the application of the Pythagorean Theorem. Each example reinforces the method and helps students recognize patterns in problem-solving, ultimately leading to a deeper understanding of the topic.
Teacher's Script: Now, let's look at our first example of a right triangle. Can you identify the two known sides? Great! We have 8 and 10. Our goal is to find the length of the hypotenuse, which we've labeled c. Remember, in a right triangle, we can use the Pythagorean Theorem to find the missing side. Let's work through this together and see how we can apply a2 + b22 = c2 to solve for c.
For a complete collection of math examples related to Right Triangles click on this link: Math Examples: Right Triangles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.B.6, CCSS.MATH.CONTENT.8.G.B.7, CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Right Triangles |
| Copyright Year | 2013 |
| Keywords | right triangles, leg, hypotenuse |