Display Title
Math Example--Right Triangles-- Example 21
Display Title
Math Example--Right Triangles-- Example 21
Topic
Right Triangles
Description
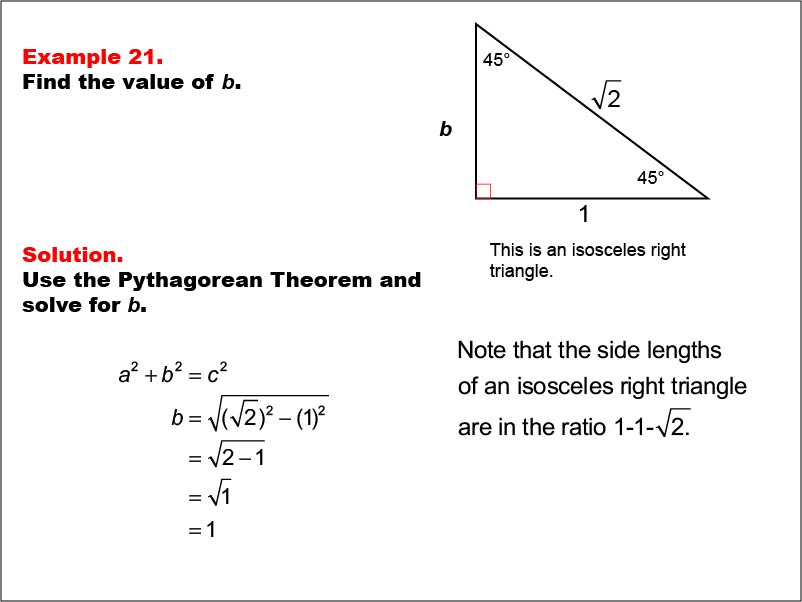
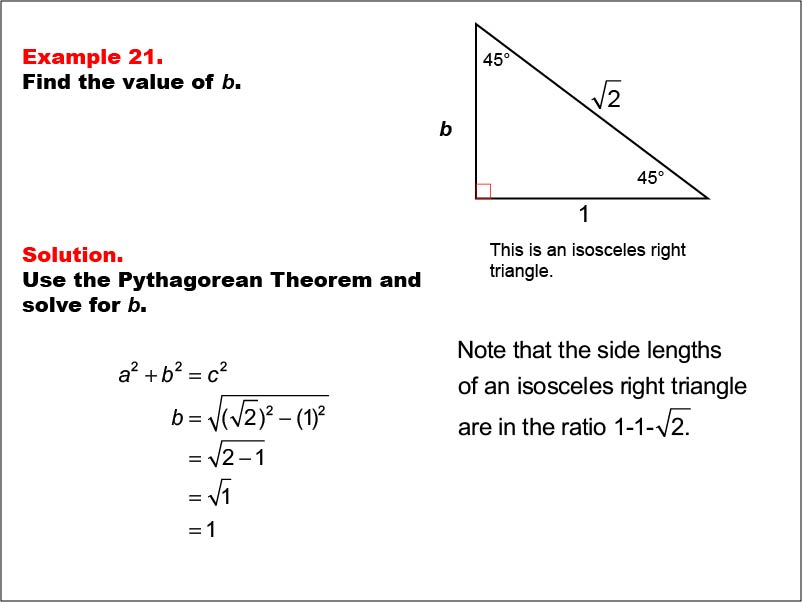
This example presents an isosceles right triangle with angles 45°, 45°, and 90°. The hypotenuse is labeled √(2), one leg is labeled 1, and the other leg is labeled b. Using the Pythagorean Theorem, we calculate that b = √((√(2))2 - 12) = sqrt(2 - 1) = √(1) = 1. This demonstrates the special properties of 45-45-90 triangles, where the legs are equal and the hypotenuse is √(2) times the length of a leg.
Isosceles right triangles are important in geometry due to their symmetry and consistent angle measures. This example reinforces the relationship between the side lengths in a 45-45-90 triangle, helping students understand the unique properties of these special right triangles.
Providing multiple worked examples is crucial for students to fully grasp the concept of right triangles and their various applications. Each new example offers an opportunity to reinforce previously learned concepts while introducing new ideas, helping students build a comprehensive understanding of right triangle geometry.
Teacher's Script: Let's examine our twenty-first example. We have an isosceles right triangle with a hypotenuse of √(2) and one leg of 1. What do you notice about the angles in this triangle? That's right, they're 45°, 45°, and 90°. Our task is to find the length of the other leg, b. As we solve this, think about why the legs of this triangle might be equal. How does this relate to the symmetry of the triangle?
For a complete collection of math examples related to Right Triangles click on this link: Math Examples: Right Triangles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.B.6, CCSS.MATH.CONTENT.8.G.B.7, CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Right Triangles |
| Copyright Year | 2013 |
| Keywords | right triangles, leg, hypotenuse |