Display Title
Math Example--Right Triangles-- Example 22
Display Title
Math Example--Right Triangles-- Example 22
Topic
Right Triangles
Description
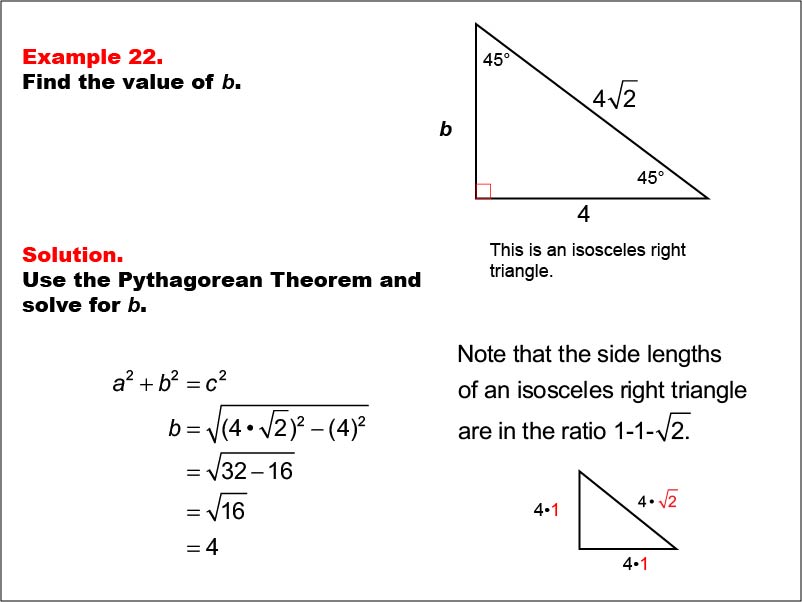
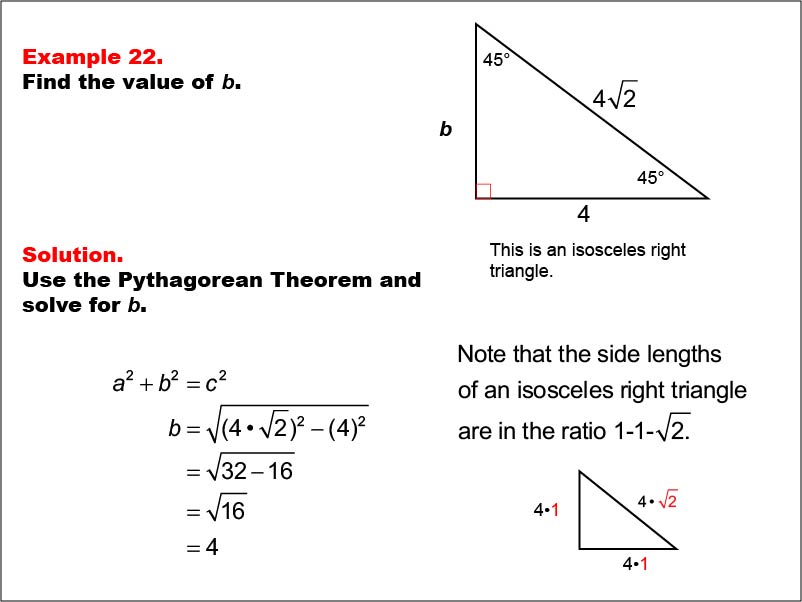
This example features an isosceles right triangle with angles 45°, 45°, and 90°. The hypotenuse is labeled 4 * √(2), one leg is labeled 4, and the other leg is labeled b. Applying the Pythagorean Theorem, we calculate that b = √((4 * √(2))2 - 42) = √(32 - 16) = 4. This demonstrates that the properties of 45-45-90 triangles hold true even when scaled.
This example builds upon the previous one, showing how the properties of isosceles right triangles remain consistent when the dimensions are scaled. It helps students understand the relationship between different sized 45-45-90 triangles and how patterns emerge in their side lengths.
Exposing students to multiple worked examples is essential for developing a comprehensive understanding of right triangles and their properties. Each new example provides an opportunity to reinforce concepts, recognize patterns, and build problem-solving skills that can be applied to more complex geometric scenarios.
Teacher's Script: Now, let's look at our twenty-second example. We have another isosceles right triangle, but this time with larger dimensions. What do you notice about the hypotenuse compared to the given leg? That's right, it's still sqrt(2) times the leg length, but everything is 4 times larger. Let's solve for b and see how this relates to our previous example. How do you think scaling affects the properties of 45-45-90 triangles?
For a complete collection of math examples related to Right Triangles click on this link: Math Examples: Right Triangles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.B.6, CCSS.MATH.CONTENT.8.G.B.7, CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Right Triangles |
| Copyright Year | 2013 |
| Keywords | right triangles, leg, hypotenuse |