Display Title
Math Example--Right Triangles-- Example 8
Display Title
Math Example--Right Triangles-- Example 8
Topic
Right Triangles
Description
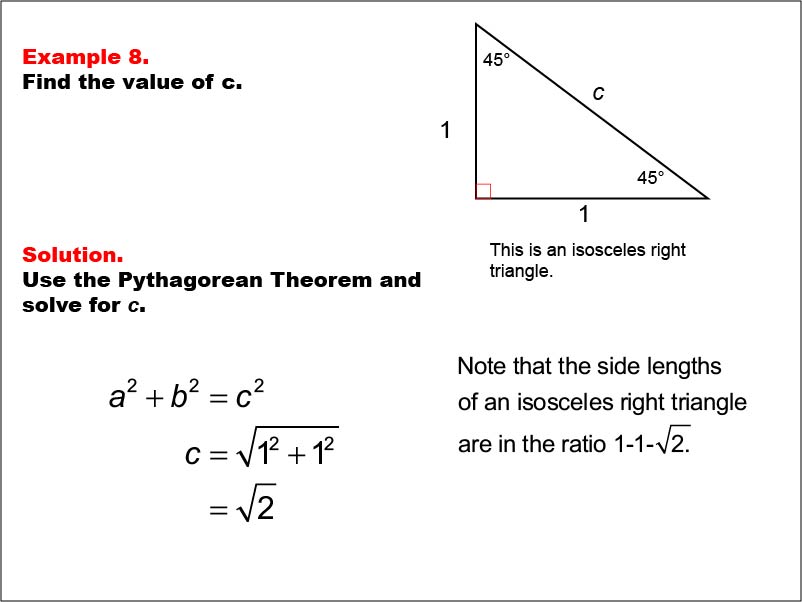
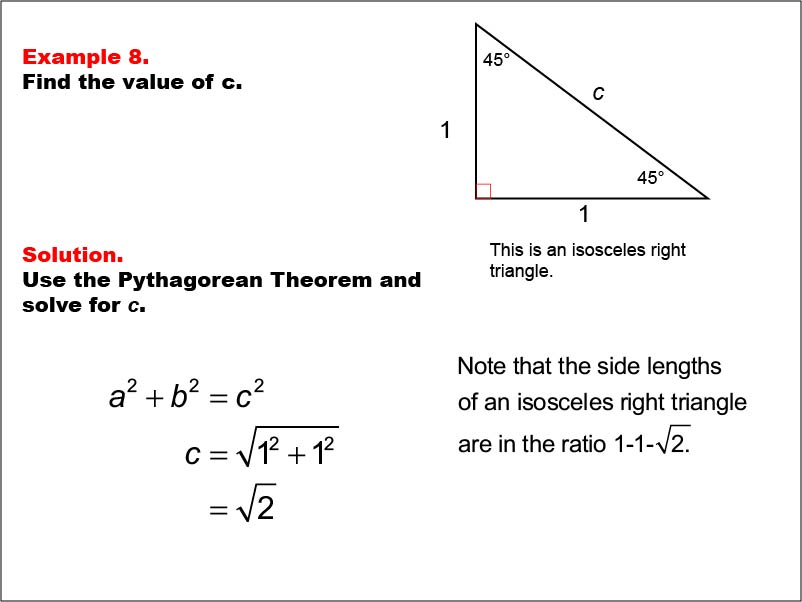
This example introduces an isosceles right triangle with legs of length 1 and an unknown hypotenuse c. The task is to find the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we calculate that c = √(12 + 12) = √(2). This triangle demonstrates the 1-1-√(2) ratio, a fundamental relationship in isosceles right triangles.
Isosceles right triangles are special cases where two sides are equal and the non-right angles are both 45 degrees. Understanding these triangles helps students grasp important concepts in geometry, such as the relationship between side lengths and angles in right triangles.
Providing multiple worked examples is crucial for students to fully comprehend the properties of right triangles, including special cases like isosceles right triangles. Each example reinforces key concepts and helps students develop problem-solving skills applicable to various geometric scenarios.
Teacher's Script: Let's examine our eighth example. We have an isosceles right triangle with legs of length 1. What makes this triangle special? That's right, it has two equal sides and two 45-degree angles. Our task is to find the length of the hypotenuse, c. How can we apply the Pythagorean Theorem here? Let's work through this together and discover the unique ratio this triangle represents.
For a complete collection of math examples related to Right Triangles click on this link: Math Examples: Right Triangles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.B.6, CCSS.MATH.CONTENT.8.G.B.7, CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Right Triangles |
| Copyright Year | 2013 |
| Keywords | right triangles, leg, hypotenuse |