Display Title
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 1
Display Title
Equations with Angles from Parallel Lines Cut by a Transversal--Example 1
Topic
Equations
Description
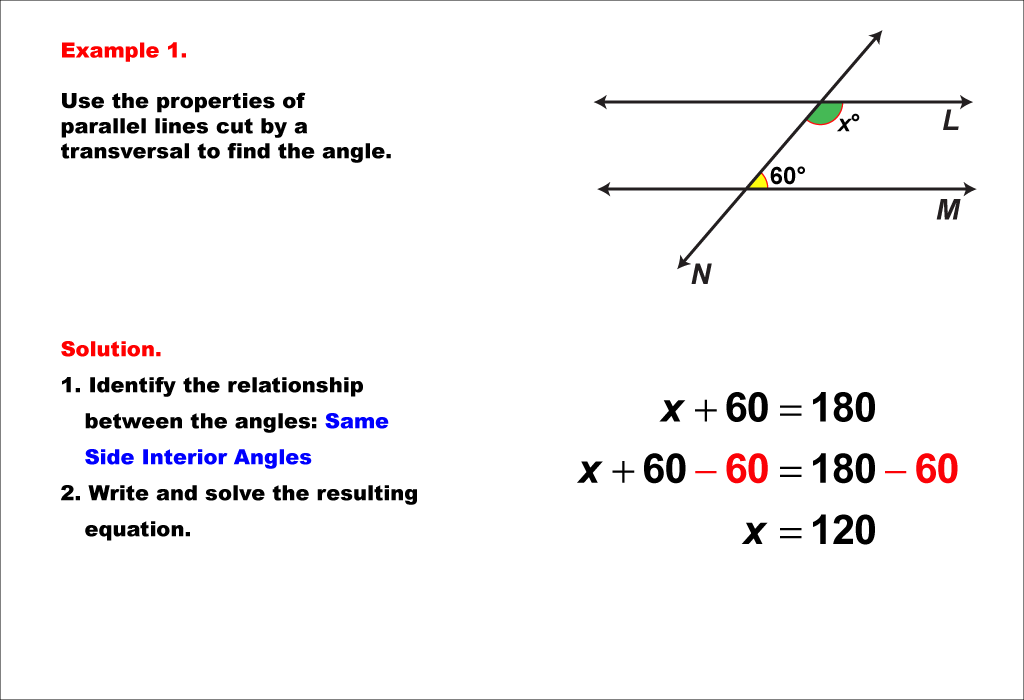
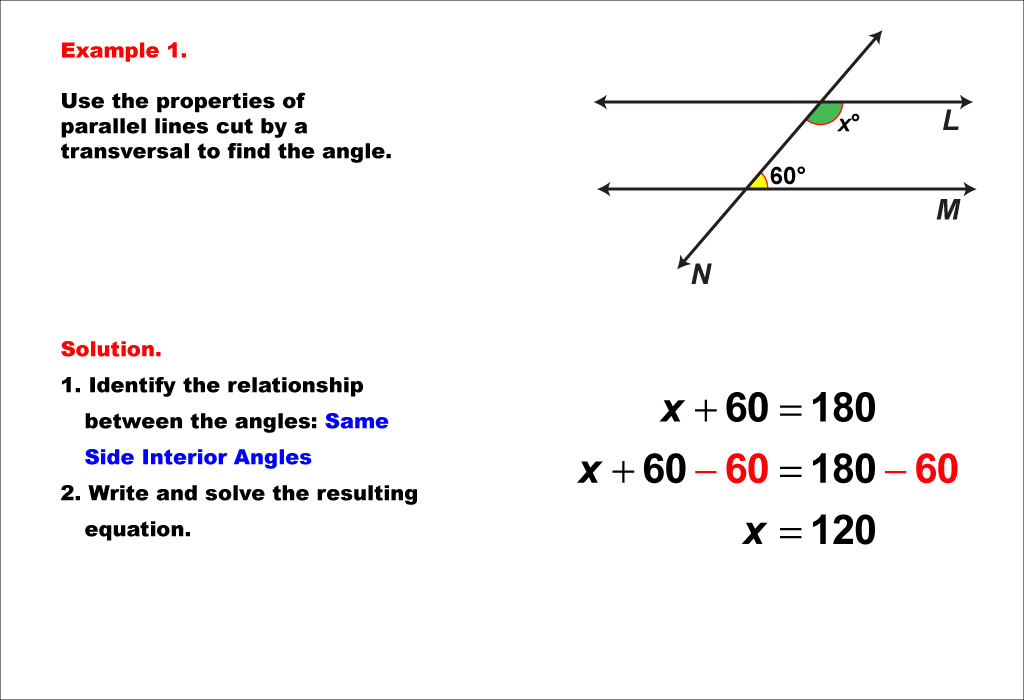
This example demonstrates solving equations involving angles formed by parallel lines cut by a transversal. Specifically, it focuses on same side interior angles. In the image, we see two parallel lines intersected by a transversal, creating eight angles. The same side interior angles are labeled as 60° and x°. The key to solving this equation lies in understanding the properties of same side interior angles in this geometric configuration. Same side interior angles are supplementary, meaning they add up to 180°. To solve for x, we set up the equation: 60 + x = 180. Subtracting 60 from both sides gives us x = 120. This solution method applies to all same side interior angle pairs in parallel lines cut by a transversal. It's crucial to recognize that this property holds true regardless of the specific angle measures, as long as the lines are parallel. This example illustrates how geometric principles can be translated into algebraic equations, bridging the gap between geometry and algebra. By understanding these relationships, students can solve more complex problems involving parallel lines and transversals, and develop a deeper appreciation for the interconnectedness of different branches of mathematics.
For a complete collection of math examples related to Equations of Parallel Lines click on this link: Math Examples: Equations of Parallel Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Angles and Planes • Applications of Angles and Planes Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities |
| Copyright Year | 2021 |
| Keywords | Parallel Lines Cut by a Transversal, parallel lines, transversal, vertical angles, supplementary angles, alternate interior angles, alternate exterior angles |