Display Title
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 3
Display Title
Topic
Equations
Description
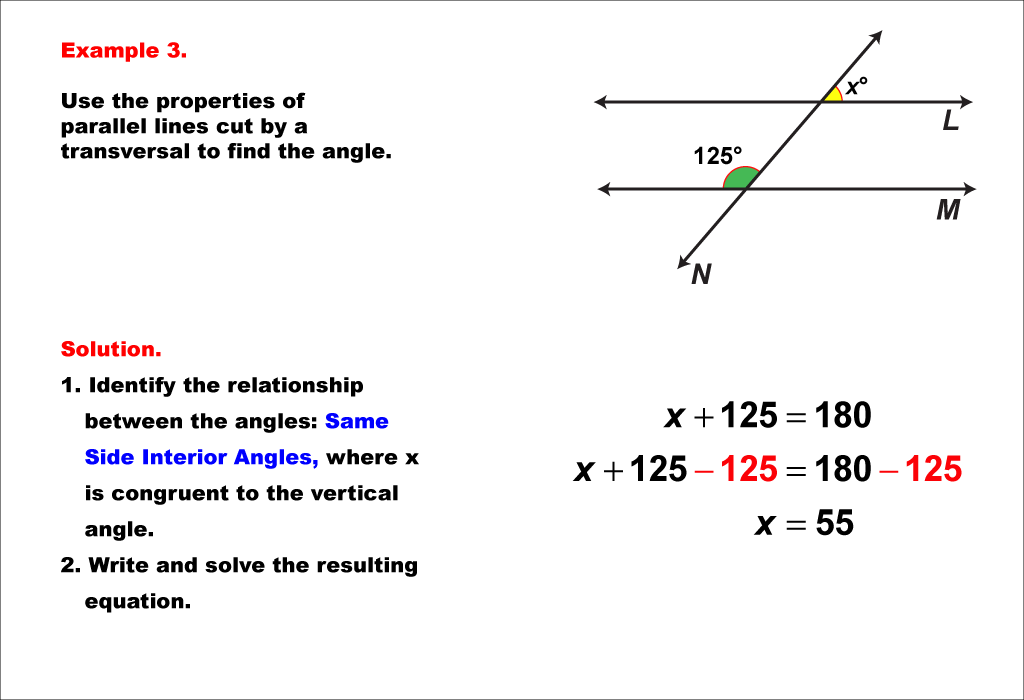
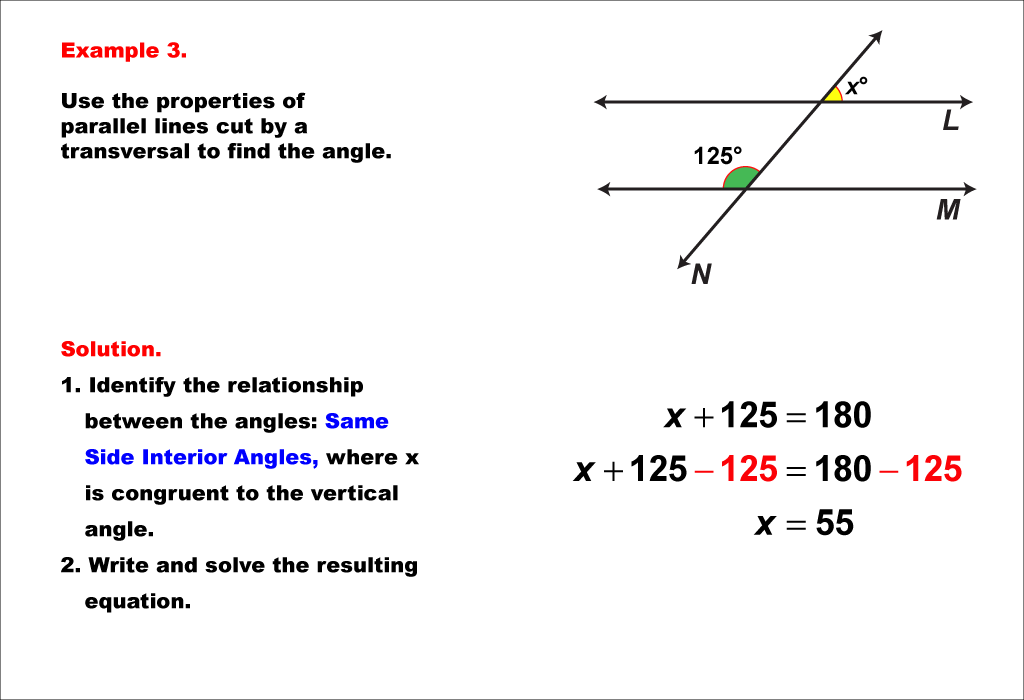
This example continues the exploration of same side interior angles in parallel lines cut by a transversal. The diagram shows two parallel lines intersected by a transversal. One angle is 125° and the other is labeled x°. The angle vertical to x is congruent and forms a pair of same side interior angles with the 125° angle. As established in previous examples, same side interior angles are supplementary, adding up to 180°. To solve for x, we set up the equation: 125 + x = 180. Subtracting 125 from both sides gives us x = 55. This example further reinforces the consistent relationship between same side interior angles in parallel lines. It's important to note that this property is bidirectional - if two lines are cut by a transversal and the same side interior angles are supplementary, then the lines must be parallel. This concept is often used in geometric proofs to establish the parallelism of lines. By working through multiple examples with different angle measures, students can internalize this fundamental property and apply it confidently in various geometric scenarios.
For a complete collection of math examples related to Equations of Parallel Lines click on this link: Math Examples: Equations of Parallel Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Angles and Planes • Applications of Angles and Planes Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities |
| Copyright Year | 2021 |
| Keywords | Parallel Lines Cut by a Transversal, parallel lines, transversal, vertical angles, supplementary angles, alternate interior angles, alternate exterior angles |