Display Title
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 4
Display Title
Equations with Angles from Parallel Lines Cut by a Transversal--Example 4
Topic
Equations
Description
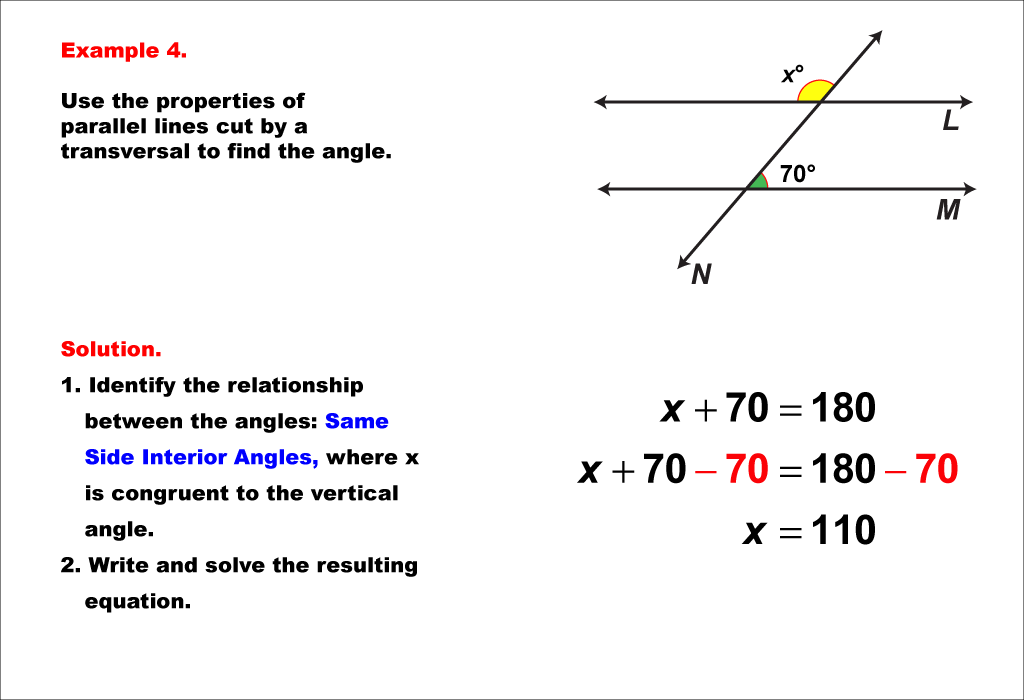
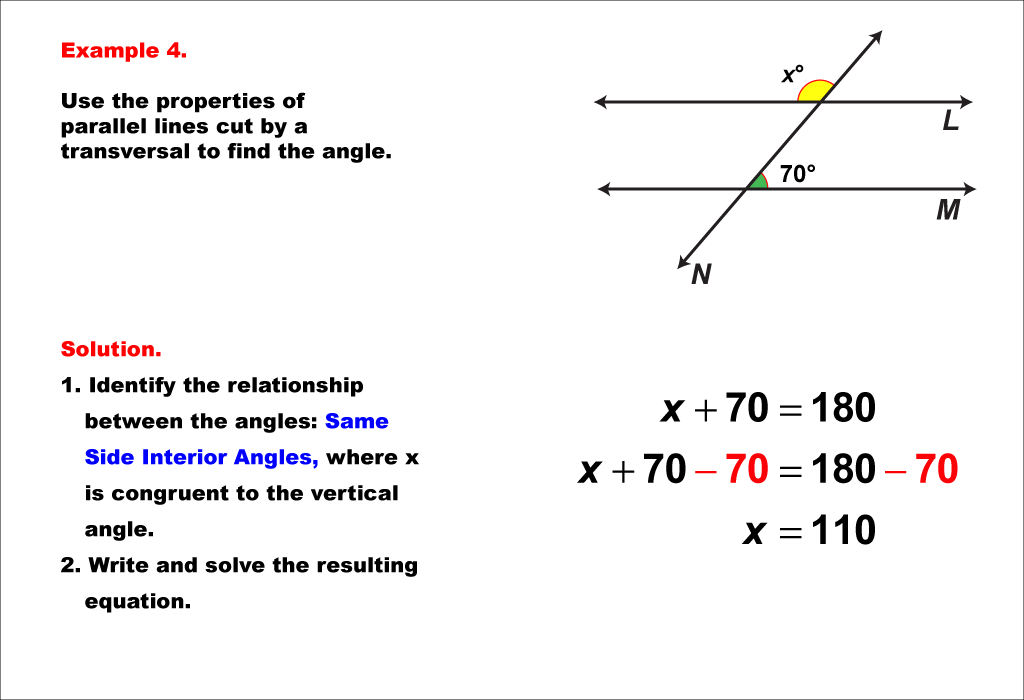
This example focuses on supplementary angles formed when parallel lines are cut by a transversal. The image shows two parallel lines intersected by a transversal, with one angle labeled as 70° and its supplementary angle as x°. We know that x and the 70° angle are supplementary because the vertical angle to x forms part of a pair of same side interior angles, which are supplementary. Supplementary angles are pairs of angles that add up to 180°. This property is crucial for solving equations involving angles in parallel line configurations. To solve for x, we set up the equation: 70 + x = 180. Subtracting 70 from both sides yields x = 110. This example demonstrates how geometric principles can be translated into algebraic equations. The supplementary angle relationship holds true for various angle pairs in this configuration, including same-side interior angles and alternate interior angles. Understanding these relationships is fundamental for solving more complex geometric problems and proofs involving parallel lines and transversals. It's worth noting that this property is a direct consequence of the parallel nature of the lines and would not hold if the lines were not parallel.
For a complete collection of math examples related to Equations of Parallel Lines click on this link: Math Examples: Equations of Parallel Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Angles and Planes • Applications of Angles and Planes Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities |
| Copyright Year | 2021 |
| Keywords | Parallel Lines Cut by a Transversal, parallel lines, transversal, vertical angles, supplementary angles, alternate interior angles, alternate exterior angles |