Display Title
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 1
Display Title
Equations Using the Exterior Angle Theorem--Example 1
Topic
Equations
Description
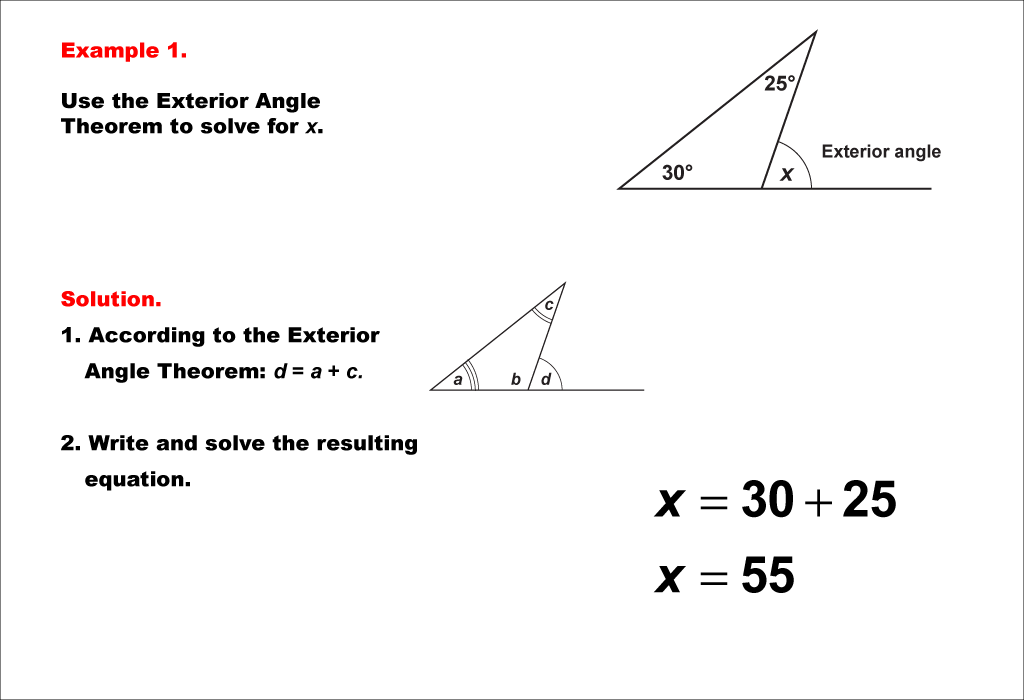
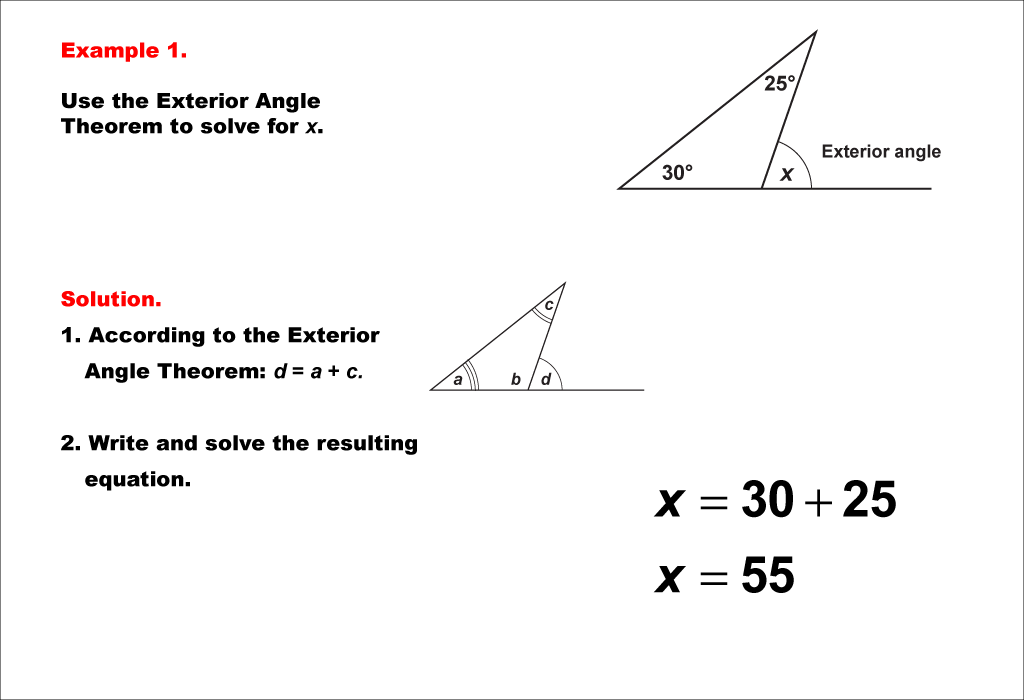
This example demonstrates the application of the Exterior Angle Theorem in solving triangle-related equations. The theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. In this case, we have a triangle with two known interior angles of 30° and 25°, while the exterior angle is represented by the variable x. The equation is set up as x = 30° + 25°, which simplifies to x = 55°. This straightforward application of the theorem allows for quick calculation of the exterior angle. The methodology for solving such equations involves identifying the known interior angles and the unknown exterior angle, then applying the theorem directly. This process relies on the fundamental geometric properties of triangles, particularly the relationships between interior and exterior angles. By understanding and applying this theorem, students can efficiently solve for unknown angles in various triangle configurations, making it a valuable tool in geometry and trigonometry. The simplicity of this example serves as an excellent introduction to more complex scenarios involving the Exterior Angle Theorem.
For a complete collection of math examples related to Equations That Use the Exterior Angle Theorem click on this link: Math Examples: Equations That Use the Exterior Angle Theorem Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2021 |
| Keywords | exterior angles, exterior angle theorem, supplementary angles |