Display Title
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 5
Display Title
Equations Using the Exterior Angle Theorem--Example 5
Topic
Equations
Description
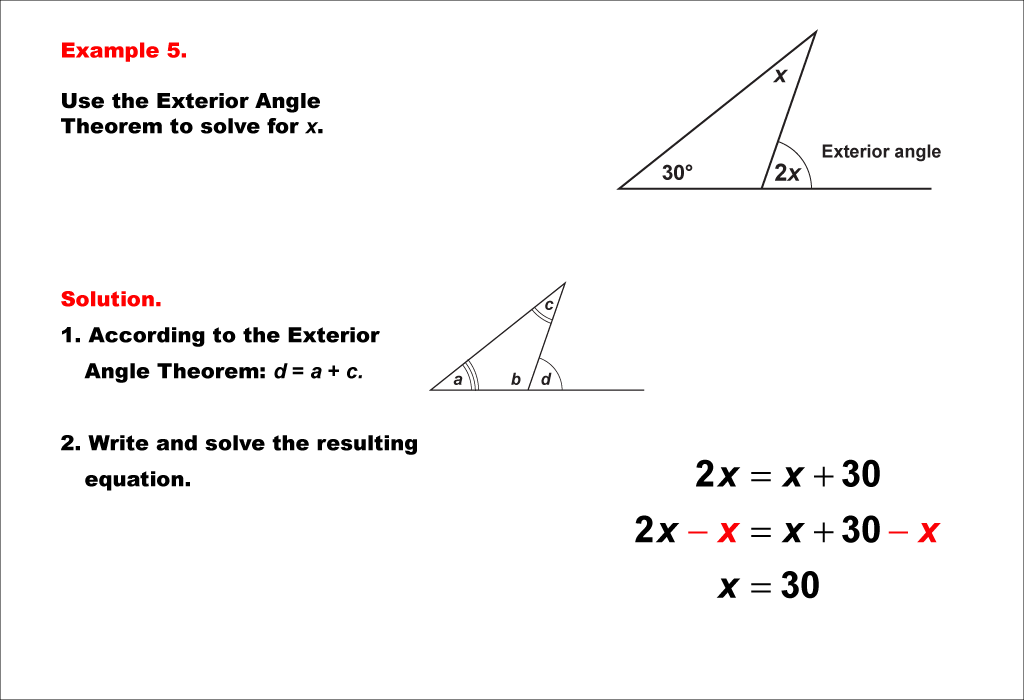
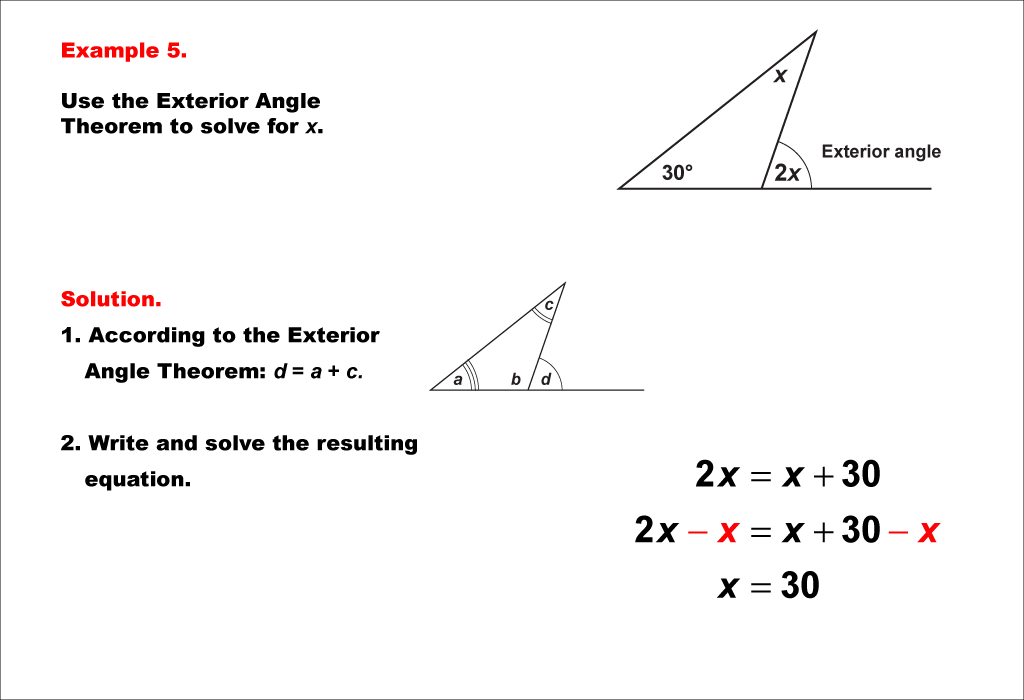
This example presents a more challenging application of the Exterior Angle Theorem. In this triangle, we have one known interior angle of 30°, an unknown interior angle x, and an exterior angle expressed as 2x. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Here, the equation is set up as 2x = 30° + x. This algebraic representation requires more sophisticated problem-solving skills. To solve for x, we first subtract x from both sides, resulting in x = 30°. Then, we can verify that the exterior angle 2x is indeed 60°, which satisfies the theorem. This problem demonstrates how the theorem can be applied in situations where the exterior angle is expressed in terms of a variable. The methodology for solving such equations involves setting up the equation based on the theorem, then using algebraic manipulation to isolate the unknown variable. This process combines geometric reasoning with more advanced algebraic skills, pushing students to think critically about the relationships between angles in a triangle. By working through this type of problem, students develop a deeper understanding of how variables can represent both interior and exterior angles, preparing them for more complex geometric and algebraic challenges.
For a complete collection of math examples related to Equations That Use the Exterior Angle Theorem click on this link: Math Examples: Equations That Use the Exterior Angle Theorem Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2021 |
| Keywords | exterior angles, exterior angle theorem, supplementary angles |