Display Title
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4
Display Title
Solving Equations with Angle Measures 2--Example 4
Topic
Equations
Description
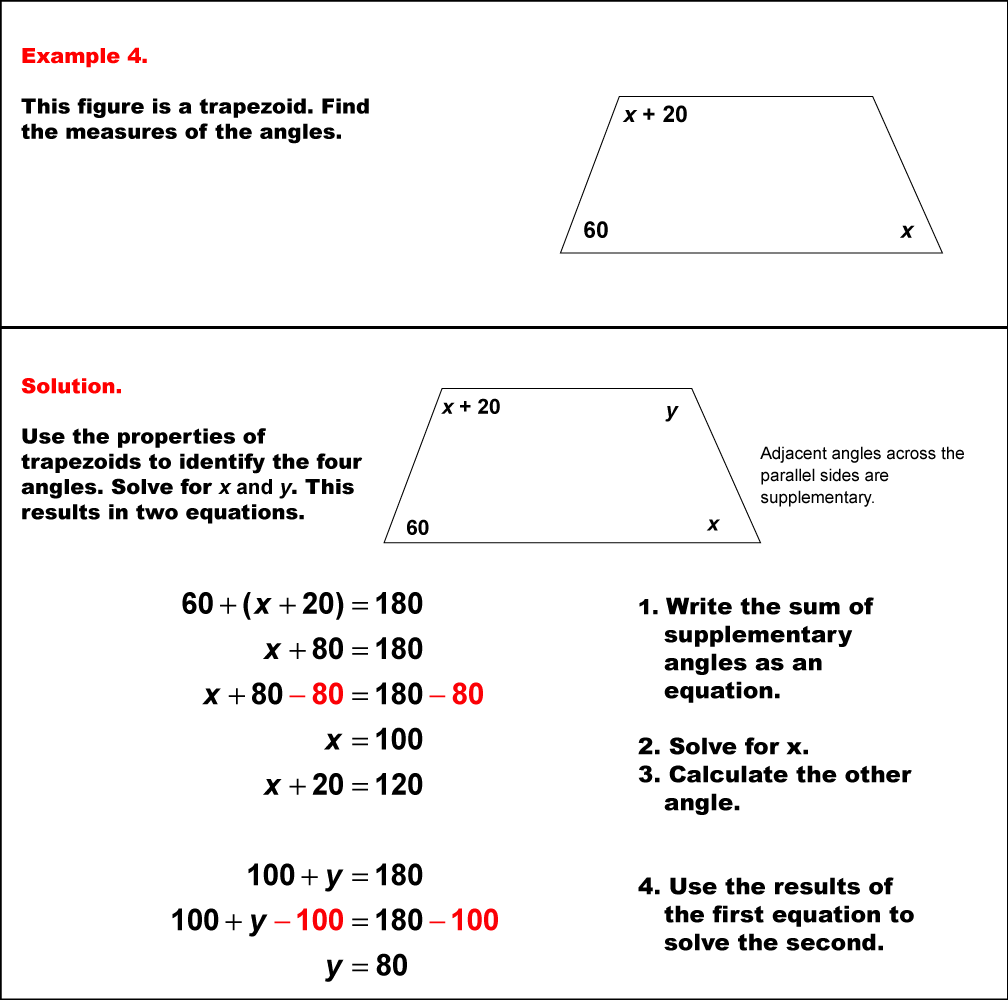
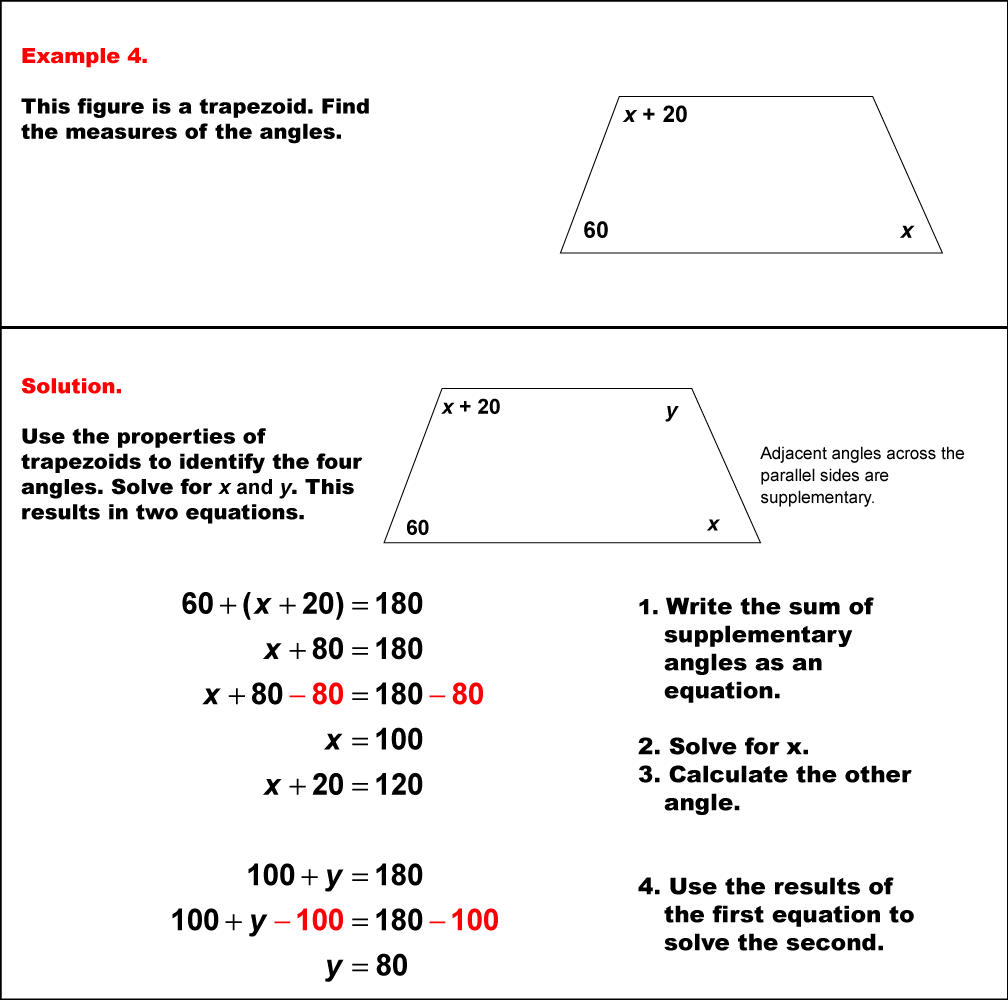
This example demonstrates solving equations involving angle measures in a trapezoid. The trapezoid has one known angle of 60° and three unknown angles represented as x°, (x+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the angles on the same side of a transversal are supplementary. We can set up two equations: 60° + x° + (x+20)° + y° = 360° and 60° + (x + 20)° = 180°. From the second equation, we can deduce that x° = 100°. Substituting this into the first equation: 60° + 100° + (100+20)° + y° = 360°. Simplifying, we get y° = 80°. Also (x+20)° = 120°. This problem showcases how to solve systems of equations in geometric contexts involving trapezoids. It reinforces the understanding of trapezoid properties and helps students develop skills in translating complex geometric relationships into multiple algebraic equations. Such problems are crucial in developing analytical thinking and preparing students for more advanced concepts in geometry and algebra.
For a complete collection of math examples related to Solving Equations with Angle Measures click on this link: Math Examples: Solving Equations with Angle Measures Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5, CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.7.EE.B.4.A, CCSS.MATH.CONTENT.7.G.B.5 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Multistep Equations Geometry • Quadrilaterals • Applications of Quadrilaterals |
| Copyright Year | 2020 |
| Keywords | quadrilaterals, equations |