Display Title
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12
Display Title
Solving Equations with Angle Measures--Example 12
Topic
Equations
Description
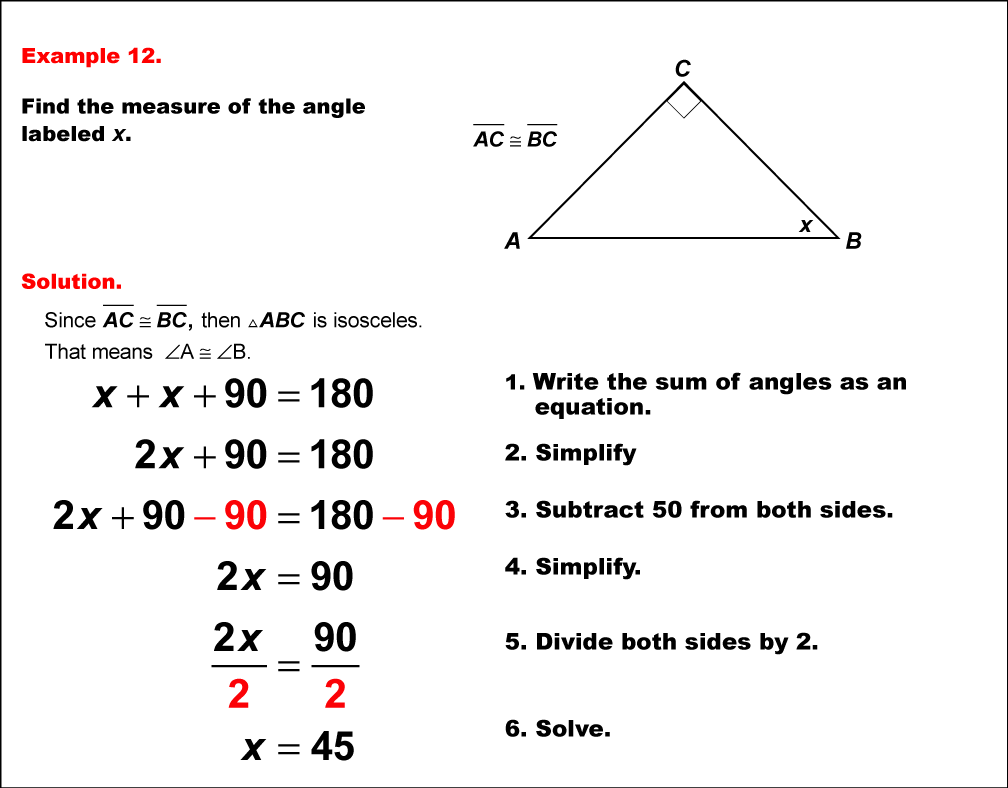
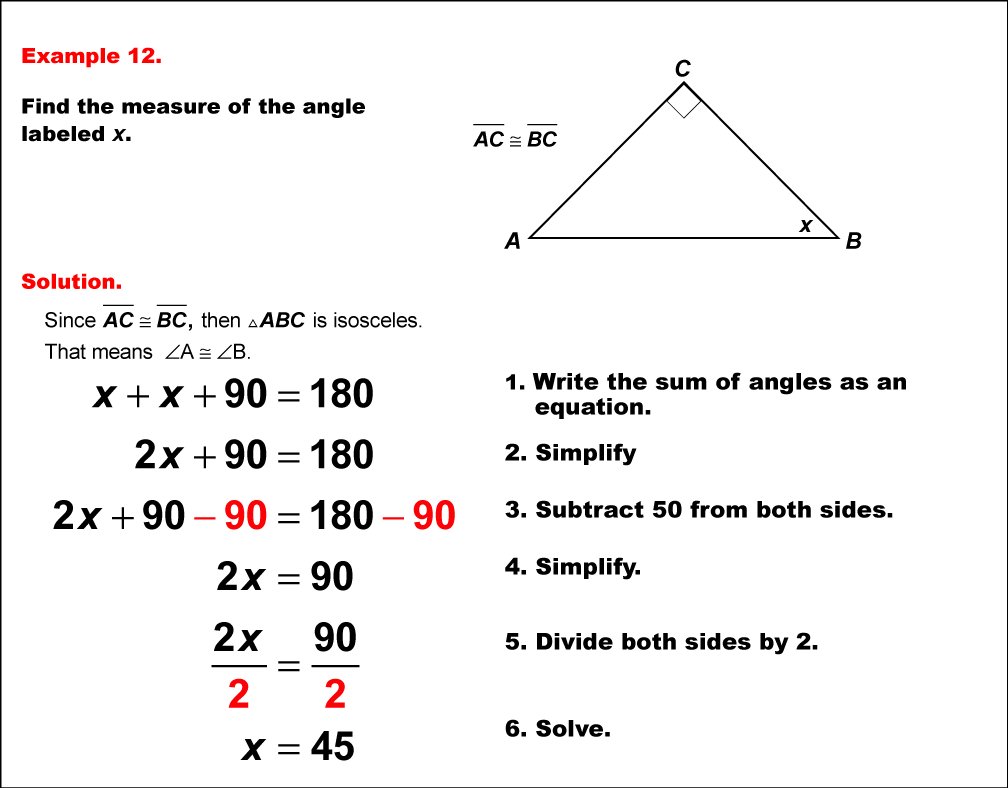
This example demonstrates solving an equation involving angle measures in an isosceles right triangle. The triangle has two equal angles represented by x° and a right angle of 90°. This problem combines properties of both isosceles and right triangles. To solve it, we apply the principles that the sum of angles in a triangle is 180°, an isosceles triangle has two equal angles, and a right triangle has one 90° angle. The equation can be set up as x° + x° + 90° = 180°. Simplifying, we get 2x° + 90° = 180°. Subtracting 90° from both sides yields 2x° = 90°. Dividing both sides by 2, we find x° = 45°. This problem is significant because it introduces the concept of the isosceles right triangle, a special case where the two non-right angles are always 45°. It helps students understand the unique properties of this triangle, including the fact that its leg-to-hypotenuse ratio is always 1:√2. Such problems are crucial in developing a deeper understanding of special right triangles, which are fundamental in trigonometry and have numerous real-world applications in fields like engineering and architecture.
For a complete collection of math examples related to Solving Equations with Angle Measures click on this link: Math Examples: Solving Equations with Angle Measures Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5, CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.7.EE.B.4.A, CCSS.MATH.CONTENT.7.G.B.5 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Multistep Equations Geometry • Angles and Planes • Applications of Angles and Planes |
| Copyright Year | 2020 |
| Keywords | angles, solving equations, triangles |