Display Title
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3
Display Title
Solving Equations with Angle Measures--Example 3
Topic
Equations
Description
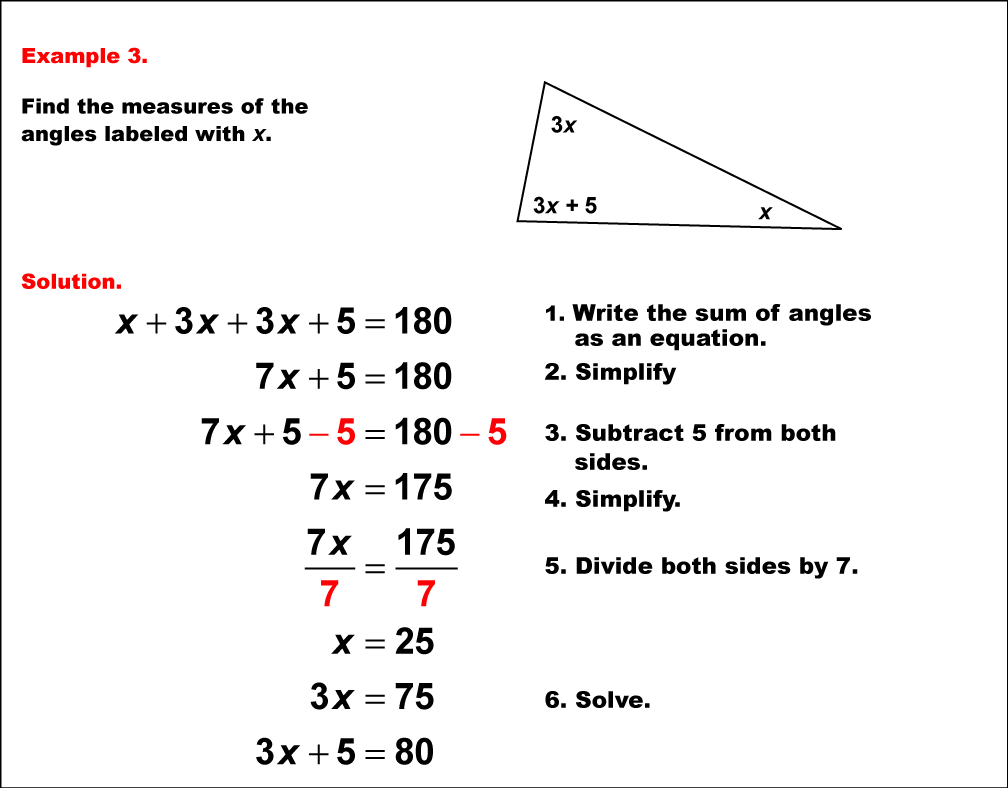
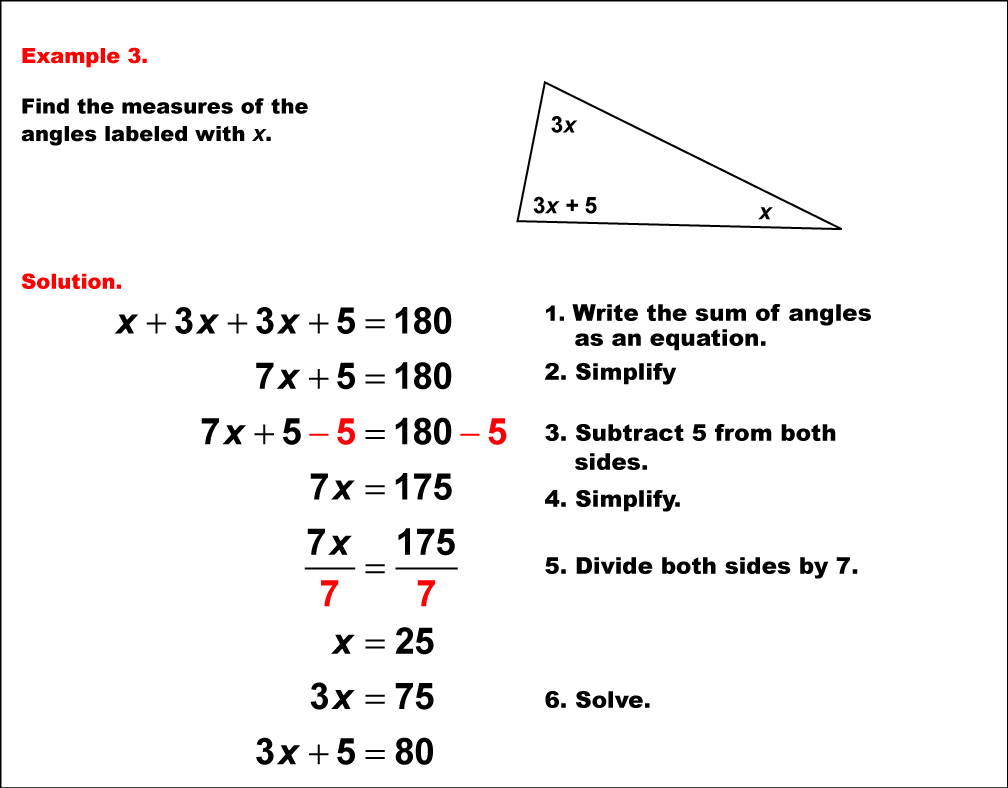
This example presents a more challenging scenario in solving equations with angle measures in a triangle. All three angles are expressed in terms of a single variable x: x°, 3x°, and (3x+5)°. To solve this problem, we apply the principle that the sum of angles in a triangle is 180°. The equation is set up as x° + 3x° + (3x+5)° = 180°. Simplifying, we get x° + 3x° + 3x° + 5° = 180°, which reduces to 7x° + 5° = 180°. Subtracting 5° from both sides yields 7x° = 175°. Dividing both sides by 7, we find x° = 25°. From this, we can calculate the three angles: 25°, 75°, and 80°. This problem demonstrates a more advanced application of algebraic skills in geometry. It requires students to manipulate expressions with variables and constants, reinforcing their understanding of how to translate complex geometric relationships into solvable equations. Such problems are crucial in developing analytical thinking and preparing students for higher-level mathematics where abstract reasoning and algebraic manipulation are essential skills.
For a complete collection of math examples related to Solving Equations with Angle Measures click on this link: Math Examples: Solving Equations with Angle Measures Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5, CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.7.EE.B.4.A, CCSS.MATH.CONTENT.7.G.B.5 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Multistep Equations Geometry • Angles and Planes • Applications of Angles and Planes |
| Copyright Year | 2020 |
| Keywords | angles, solving equations, triangles |