Display Title
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9
Display Title
Solving Equations with Angle Measures--Example 9
Topic
Equations
Description
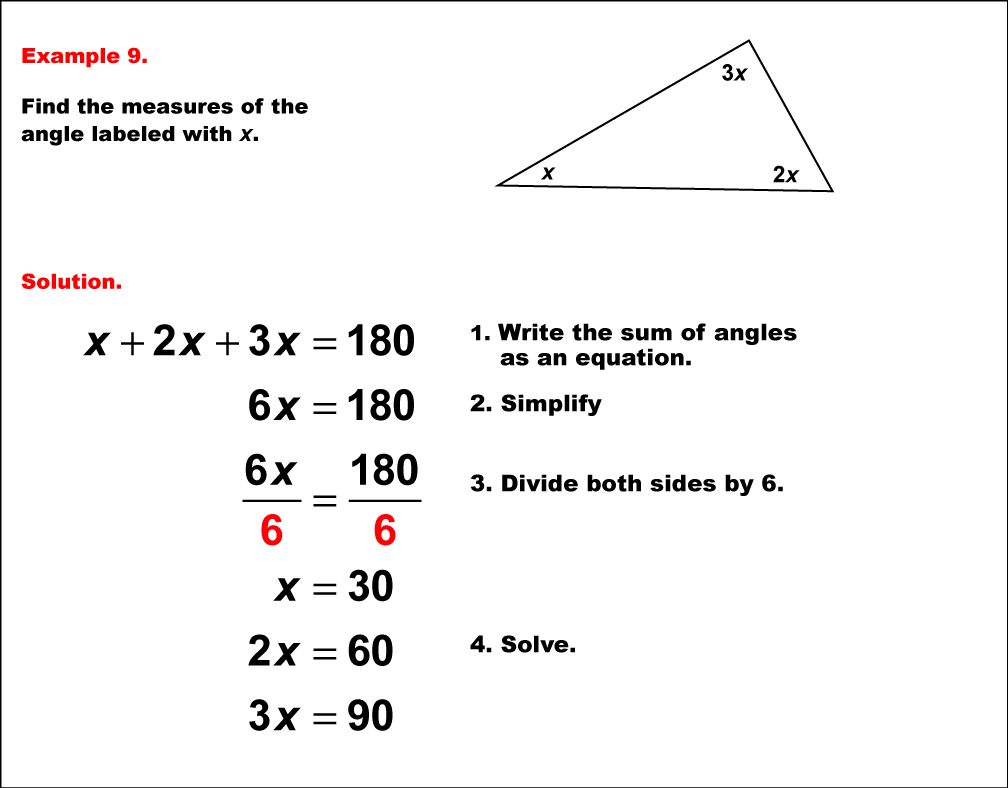
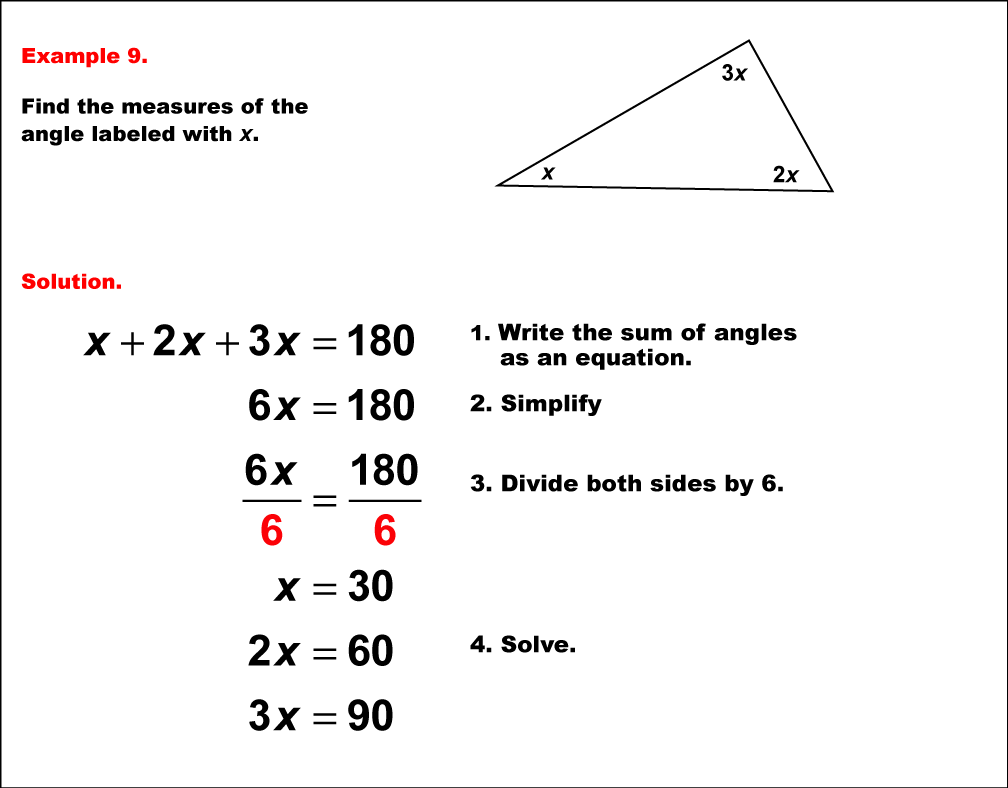
This example illustrates solving an equation involving angle measures in a triangle where all angles are expressed in terms of a single variable. The triangle has angles represented as x°, 2x°, and 3x°. To solve this problem, we apply the fundamental principle that the sum of angles in a triangle is always 180°. We can set up the equation: x° + 2x° + 3x° = 180°. Simplifying, we get 6x° = 180°. Dividing both sides by 6, we find x° = 30°. Therefore, the three angles of the triangle are 30°, 60°, and 90°. This problem showcases a more advanced application of algebraic skills in geometry. It requires students to manipulate expressions with variables and reinforces the concept that even when angles are expressed in terms of a variable, they must still adhere to the properties of triangles. Interestingly, this problem results in a 30-60-90 triangle, a special right triangle with well-known properties. Such problems are crucial in developing analytical thinking and preparing students for more complex geometric and algebraic concepts. They also help students understand the relationship between different angles in a triangle and how they can be represented algebraically.
For a complete collection of math examples related to Solving Equations with Angle Measures click on this link: Math Examples: Solving Equations with Angle Measures Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.A.5, CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.7.EE.B.4.A, CCSS.MATH.CONTENT.7.G.B.5 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Multistep Equations Geometry • Angles and Planes • Applications of Angles and Planes |
| Copyright Year | 2020 |
| Keywords | angles, solving equations, triangles |