Display Title
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 2
Display Title
Solving Equations Using Triangle Properties: Example 2
Topic
Equations
Description
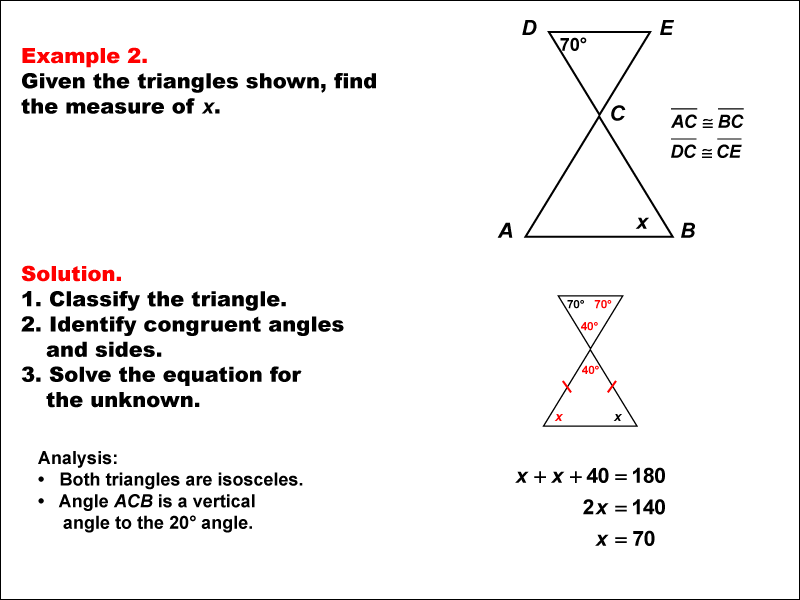
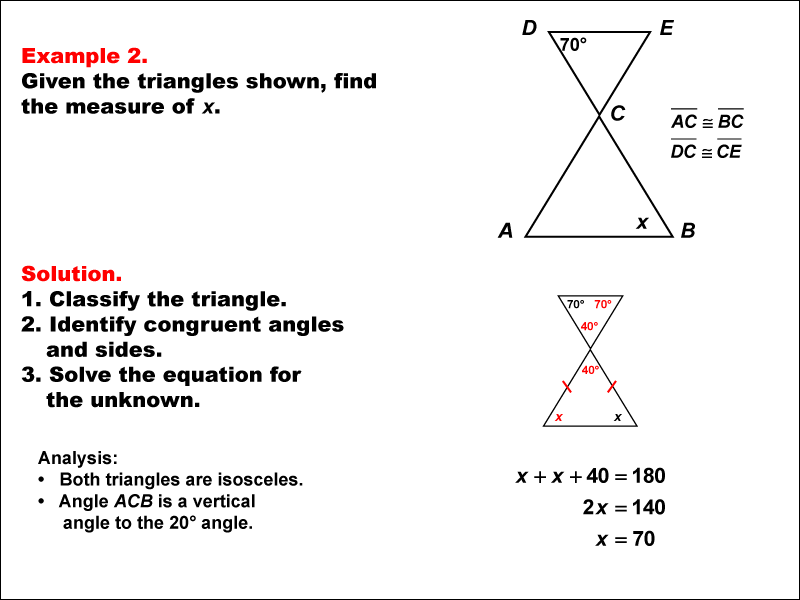
This example explores solving equations using the properties of similar isosceles triangles, building upon the concepts introduced in Example 1. In this case, we have two similar isosceles triangles with one known angle of 70° and an unknown angle x. The goal is to determine the value of x using triangle properties and algebraic techniques.
Isosceles triangles have two equal sides and two equal base angles. When dealing with similar isosceles triangles, we can leverage additional properties: Corresponding angles in similar triangles are equal. The ratio of corresponding sides in similar triangles is constant. The sum of angles in any triangle is 180°.
To solve this type of equation, we follow these steps: Identify the known angle (70°) in the top triangle and its position in the triangle. Recognize that in an isosceles triangle, the base angles are equal. Set up an equation using the fact that the sum of angles in a triangle is 180°. Solve the resulting linear equation for the unknown apex angle y. In this specific example, we can deduce that the 70° angle is one of the base angles of the isosceles triangle. Since base angles in an isosceles triangle are equal, the other base angle must also be 70°. The apex angle of the isosceles triangle would then be x°. Using the property that the sum of angles in a triangle is 180°, we can set up the equation: y + 70 + 70 = 180 Solving this equation gives us y = 40°.
This 40° angle is vertical to the apex angle of the bottom triangle. So to find the value of x solve the equation x + x + 40 = 180, which results in x = 70.
This solution demonstrates how the properties of isosceles triangles and similar triangles can be combined to solve geometric equations. It also illustrates the practical application of algebraic concepts in geometry, reinforcing the interconnectedness of different mathematical domains.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.HSA.CED.A.1 |
|---|---|
| Grade Range | 9 - 11 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2022 |
| Keywords | triangles, solving equations |