Display Title
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5
Display Title
Solving Equations Using Triangle Properties: Example 5
Topic
Equations
Description
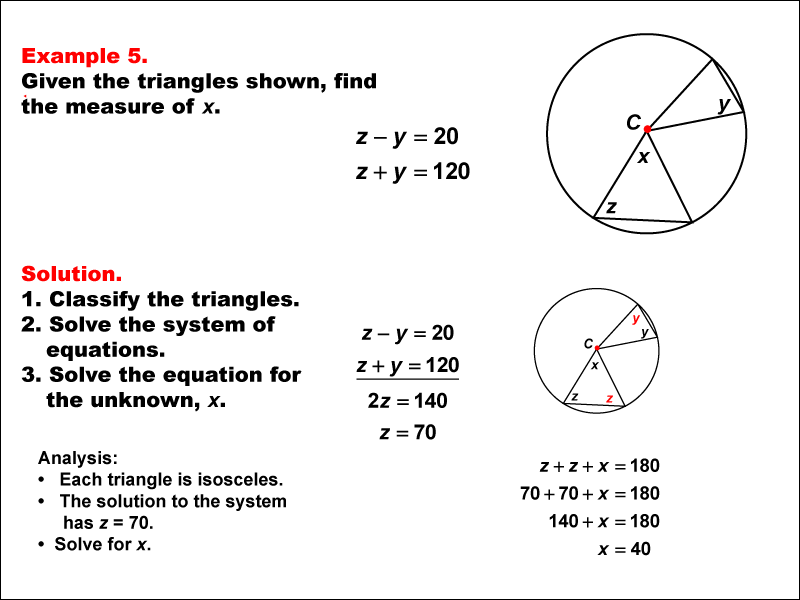
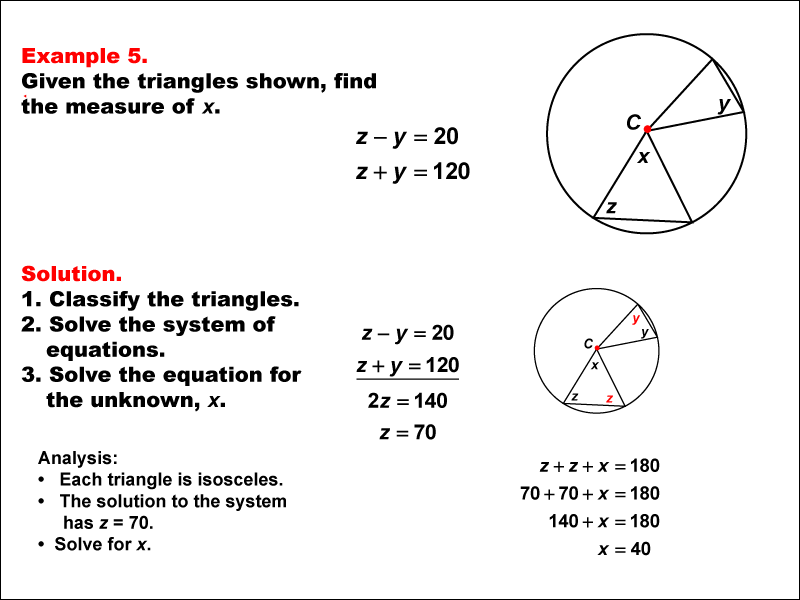
This example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles.
Isosceles triangles centered in a circle have several important properties: The base angles of an isosceles triangle are equal. The line from the center of the circle to the midpoint of the base is perpendicular to the base. The central angle is twice the inscribed angle that subtends the same arc. To solve this system of equations, we can use the substitution or elimination method:
Given equations:
z - y = 20 (Equation 1)
z + y = 120 (Equation 2)
Add the equations to eliminate y:
(z - y) + (z + y) = 20 + 120
2z = 140
Solve for z:
z = 70
Solve for x by using the property of isosceles triangles. We get 70 + 70 + x = 180, or x = 40°.
This example demonstrates how algebraic techniques can be applied to solve geometric problems involving isosceles triangles and circles. It highlights the importance of understanding both the algebraic methods for solving systems of equations and the geometric properties of isosceles triangles and circles. This integration of algebra and geometry is a key aspect of mathematical problem-solving, showing how different areas of mathematics are interconnected.
For a complete collection of math examples related to Equations Using Triangle Properties click on this link: Math Examples: Equations Using Triangle Properties Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.HSA.CED.A.1 |
|---|---|
| Grade Range | 9 - 11 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2022 |
| Keywords | triangles, solving equations |