Display Title
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7
Display Title
Solving Equations Using Triangle Properties: Example 7
Topic
Equations
Description
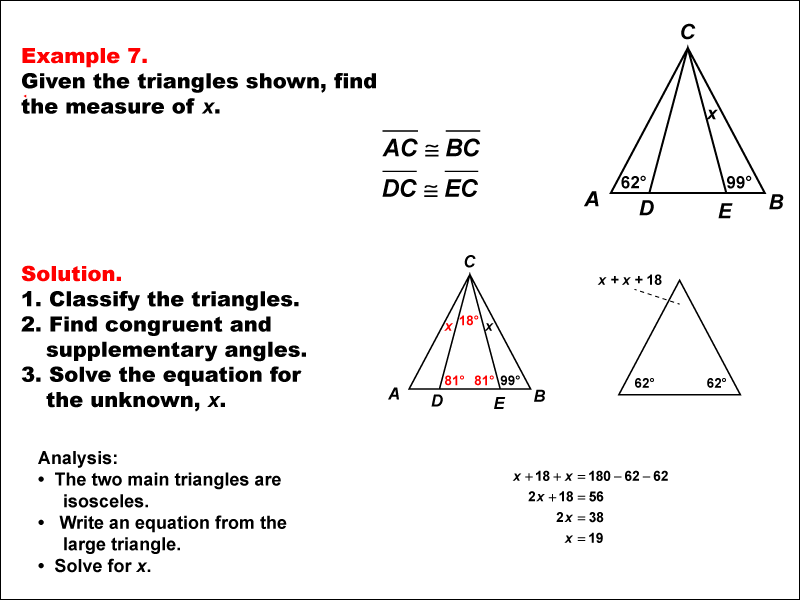
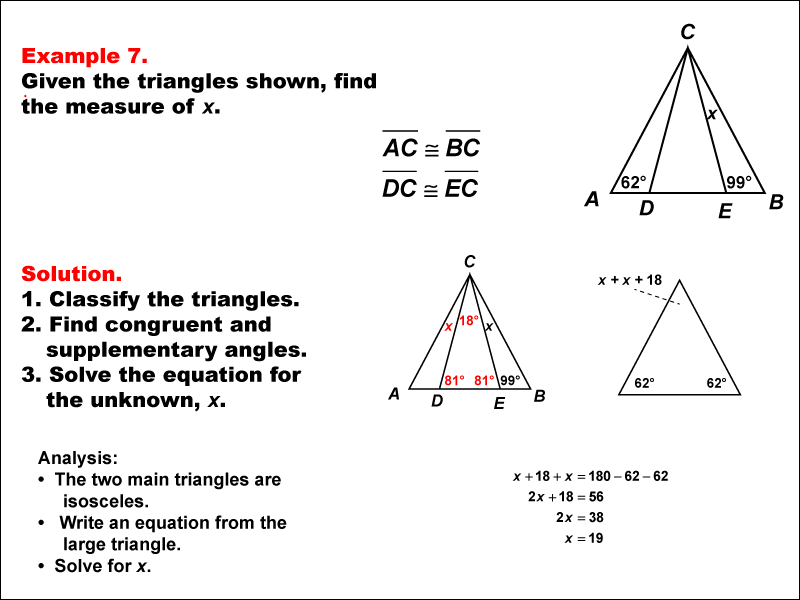
This example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle.
Key properties to consider:
- In an isosceles triangle, the base angles are equal.
- The sum of angles in any triangle is 180°.
There are two isosceles triangles that share a vertex. The 99° angle is supplementary to one of the base angles of the smaller isosceles triangle. You can see that the base angles of the smaller isosceles triangle is 81°. This also means the apex angle of the smaller isosceles triangle is 18°.
The larger triangle has base angles of 62°. This means the apex angle of the larger isoscels triange is:
180 - 62 - 62 = 56°
We can now derive this equation for the apex angle of the larger triangle:
x + 18 + x = 56
x = 19°
This example highlights the importance of analyzing geometric figures to identify important relationships. It also demonstrates how geometric properties of isosceles triangles can be used to formulate and solve equations.
For a complete collection of math examples related to Equations Using Triangle Properties click on this link: Math Examples: Equations Using Triangle Properties Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.HSA.CED.A.1 |
|---|---|
| Grade Range | 9 - 11 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2022 |
| Keywords | triangles, solving equations |