Display Title
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8
Display Title
Solving Equations Using Triangle Properties: Example 8
Topic
Equations
Description
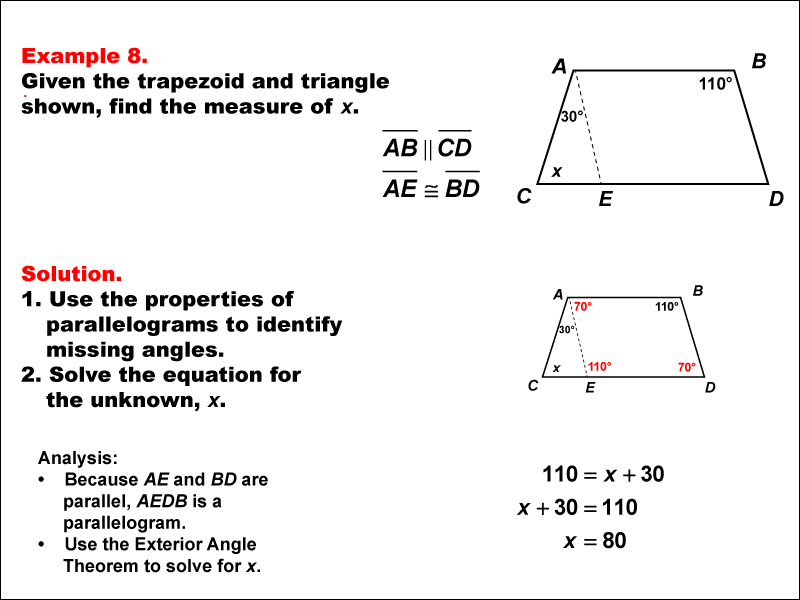
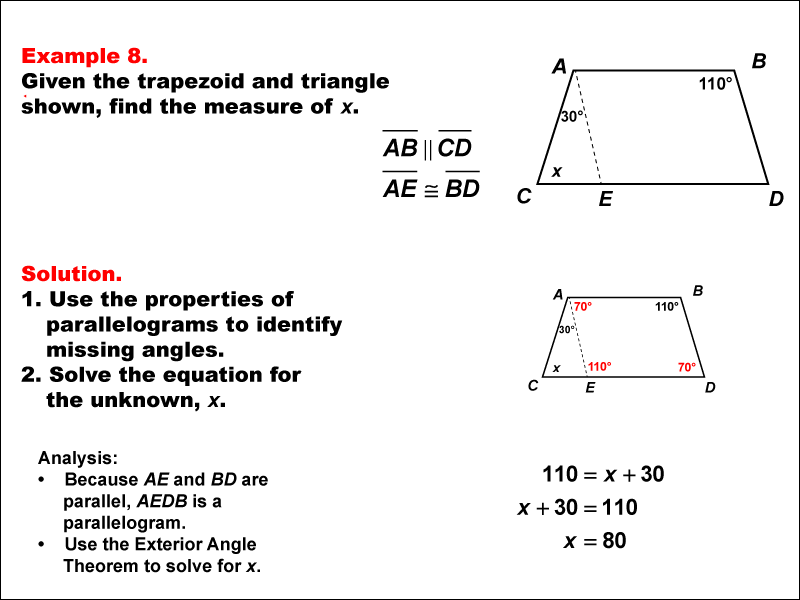
This example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation.
Key properties to consider:
- The sum of angles in a triangle is 180°.
- The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
- Opposite angles in a parallelogram are equal.
- An isosceles triangle has congruent base angles.
We form an isosceles triangle with x as one of the base angles. The exterior angle of this isosceles triangle is congruent to the 110° angle. Using the exterior angle theorem, we get:
x + 30 = 110
x = 80°
This example highlights the interconnectedness of various geometric properties and how they can be used together in problem-solving. The problem also illustrates the importance of spatial reasoning and the ability to recognize and apply relevant geometric theorems in complex figures. It reinforces the idea that understanding fundamental geometric principles can lead to solving more intricate problems involving compound shapes.
For a complete collection of math examples related to Equations Using Triangle Properties click on this link: Math Examples: Equations Using Triangle Properties Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.HSA.CED.A.1 |
|---|---|
| Grade Range | 9 - 11 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2022 |
| Keywords | triangles, solving equations |