Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4
Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4
Topic
Solving Equations
Description
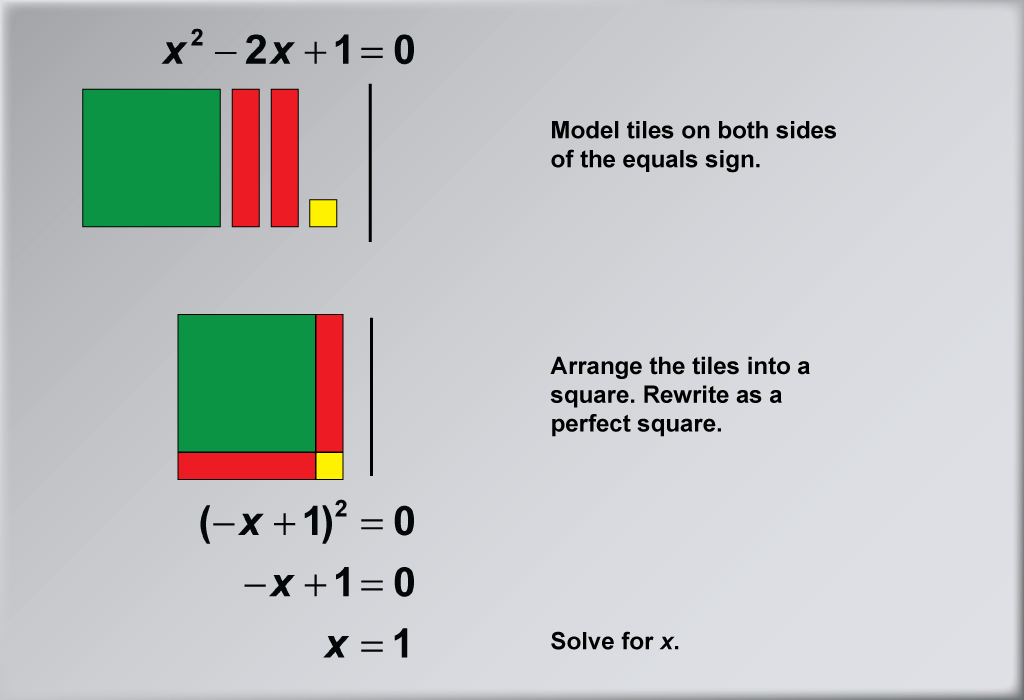
In this example, we explore solving the quadratic equation x2 - 2x + 1 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a perfect square, effectively transforming the equation into (-x + 1)2 = 0. This method showcases the versatility of algebra tiles in handling equations with both positive and negative terms, as well as illustrating the completing the square technique.
Algebra tiles provide a powerful visual and tactile approach to understanding quadratic equations. This method is particularly effective for students who struggle with abstract algebraic concepts, as it allows them to manipulate physical objects and see the relationships between terms. The use of different colored tiles for positive and negative values helps reinforce the concept of opposites and how they interact in equations, especially when dealing with subtraction.
Exposure to multiple worked-out examples is crucial for students to develop a deep understanding of solving quadratic equations. Each example in this collection presents a unique scenario, helping students recognize patterns and adapt their problem-solving strategies. This repetition with variations strengthens their ability to apply these concepts to new and more complex problems they may encounter in the future, building their confidence and mathematical intuition.
Teacher Script: "Let's examine another quadratic equation using algebra tiles. This time, we have subtraction in our equation. How does this change our approach? Notice how we use different colored tiles to represent positive and negative terms. As we arrange these tiles into a perfect square, think about how this visual representation relates to the algebraic steps we take when solving quadratic equations. Can you predict what our perfect square trinomial will look like based on the tiles we have? Remember, our goal is to rewrite the equation as (-x + 1)2 = 0, which leads us to the solution x = 1."
For a complete collection of math examples related to Solving Quadratic Equations with Algebra Tiles click on this link: Math Examples: Quadratic Equations with Algebra Tiles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.B.4 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | solving equations, algebra tiles, quadratic equations |