Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5
Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5
Topic
Solving Equations
Description
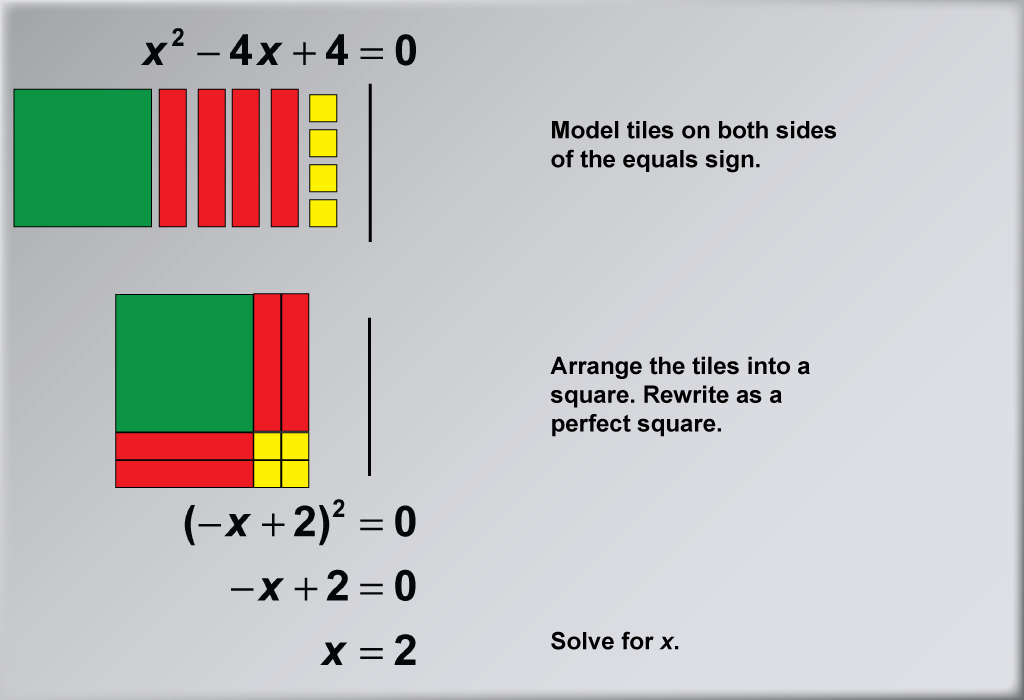
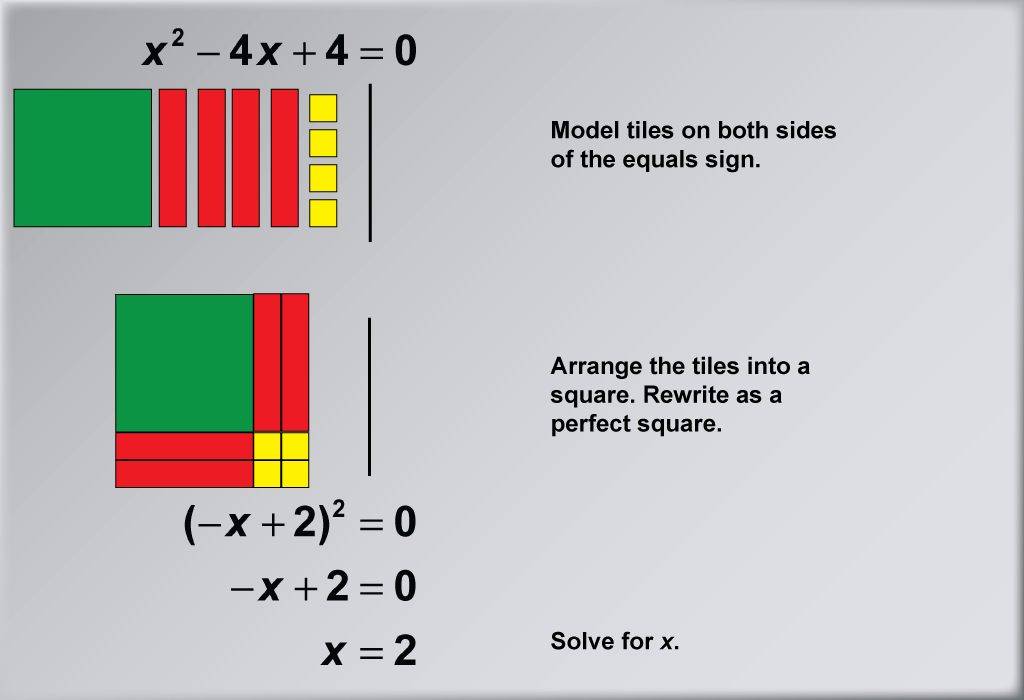
This example demonstrates the process of solving the quadratic equation x2 - 4x + 4 = 0 using algebra tiles. The visual representation shows how to arrange the tiles to form a perfect square, illustrating the completing the square method. By organizing the tiles, students can physically see how the terms combine to form the expression (-x + 2)2 = 0, making the solution process more intuitive and accessible.
Algebra tiles serve as an excellent tool for teaching quadratic equations, especially when dealing with negative terms and larger coefficients. This hands-on approach allows students to visualize and manipulate the components of the equation, reinforcing their understanding of algebraic concepts. The color-coded tiles help distinguish between positive and negative terms, making it easier for students to grasp the idea of balancing equations and combining like terms.
Presenting multiple worked-out examples is essential for students to develop a comprehensive understanding of solving quadratic equations. Each example in this collection offers a unique scenario, helping students recognize patterns and adapt their problem-solving strategies. This repetition with variations strengthens their ability to apply these concepts to new and more challenging problems they may encounter in the future.
Teacher Script: "Now, let's tackle a quadratic equation with larger negative terms using algebra tiles. How does having more negative x tiles change our approach? As we arrange these tiles into a square, think about how this visual representation relates to the algebraic steps we take when solving quadratic equations. Can you see how the negative terms affect the formation of our perfect square trinomial? This example will help you understand how to handle more complex quadratic equations with confidence. Remember, our goal is to rewrite the equation as (-x + 2)2 = 0, which leads us to the solution x = 2."
For a complete collection of math examples related to Solving Quadratic Equations with Algebra Tiles click on this link: Math Examples: Quadratic Equations with Algebra Tiles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.B.4 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | solving equations, algebra tiles, quadratic equations |