Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6
Display Title
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6
Topic
Solving Equations
Description
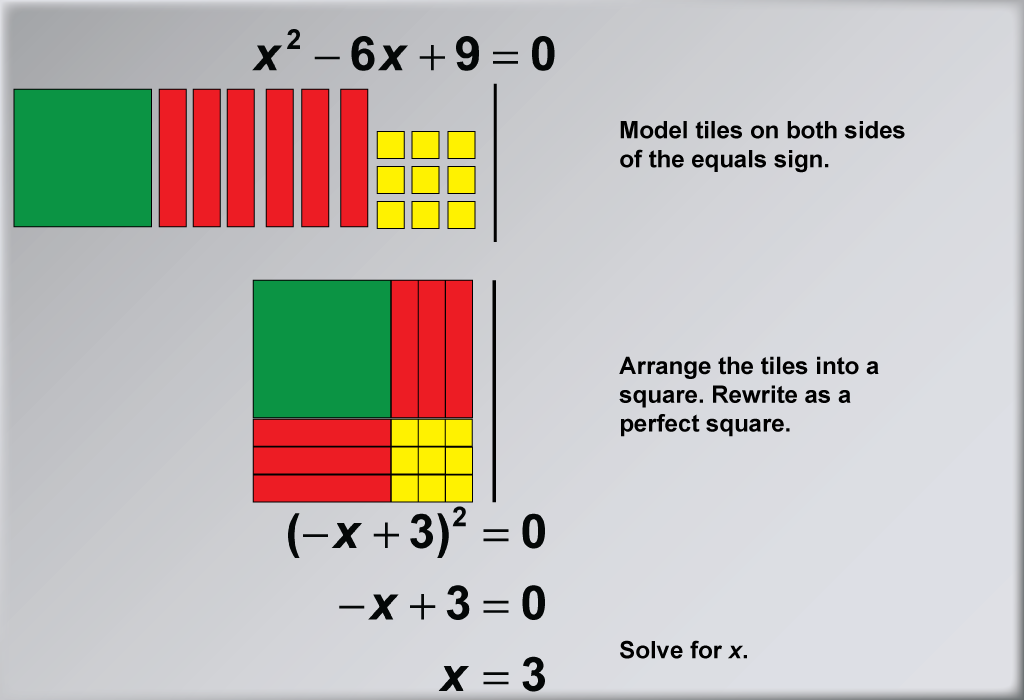
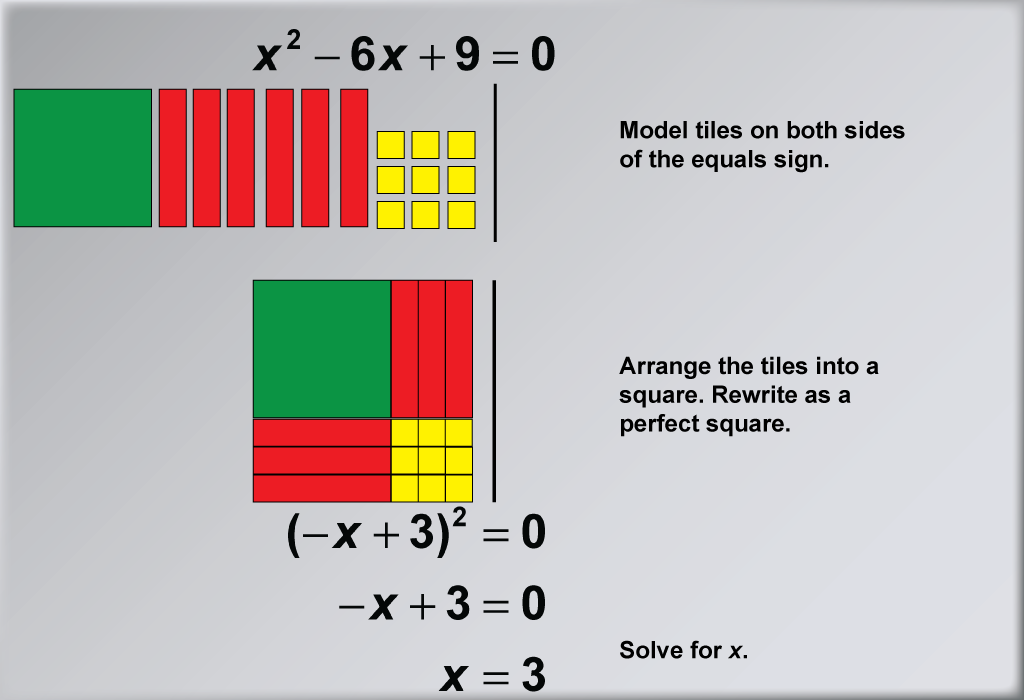
This example illustrates the process of solving the quadratic equation x2 - 6x + 9 = 0 using algebra tiles. By modeling tiles on both sides of the equation, students can visually understand the principle of maintaining equality while manipulating the equation. The tiles are arranged into a square to form a perfect square trinomial, demonstrating the completing the square method in a tangible way.
Algebra tiles serve as an excellent tool for teaching the fundamental principles of equation solving, particularly for quadratic equations. This hands-on method allows students to physically see and manipulate the components of an equation, reinforcing the concept of balance and equality. By using tiles on both sides of the equation, students can better grasp the idea that whatever operation is performed on one side must be mirrored on the other side to maintain the equation's integrity.
Presenting multiple worked-out examples is essential for students to develop a comprehensive understanding of solving quadratic equations. Each example in this collection offers a unique perspective on the problem-solving process, helping students recognize patterns and adapt their strategies. This repetition with variations strengthens their ability to apply these concepts to new and more challenging problems they may encounter in the future, building their confidence and mathematical reasoning skills.
Teacher Script: "Let's focus on balancing both sides of the equation using algebra tiles. Notice how we have tiles on both sides of the equals sign. As we manipulate these tiles, remember that whatever we do to one side of the equation, we must do to the other side as well. How does this visual representation help you understand the algebraic steps we take when solving equations? As we arrange the tiles into a square, can you see how this forms a perfect square trinomial? Our goal is to rewrite the equation as (-x + 3)2 = 0, which leads us to the solution x = 3. This example will help you develop a deeper understanding of the principles behind equation solving, which you can apply to more complex problems in the future."
For a complete collection of math examples related to Solving Quadratic Equations with Algebra Tiles click on this link: Math Examples: Quadratic Equations with Algebra Tiles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.B.4 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | solving equations, algebra tiles, quadratic equations |