Display Title
Math Example--Special Functions--Cube Root Functions in Tabular and Graph Form: Example 6
Display Title
Math Example--Special Functions--Cube Root Functions in Tabular and Graph Form: Example 6
Topic
Special Functions
Description
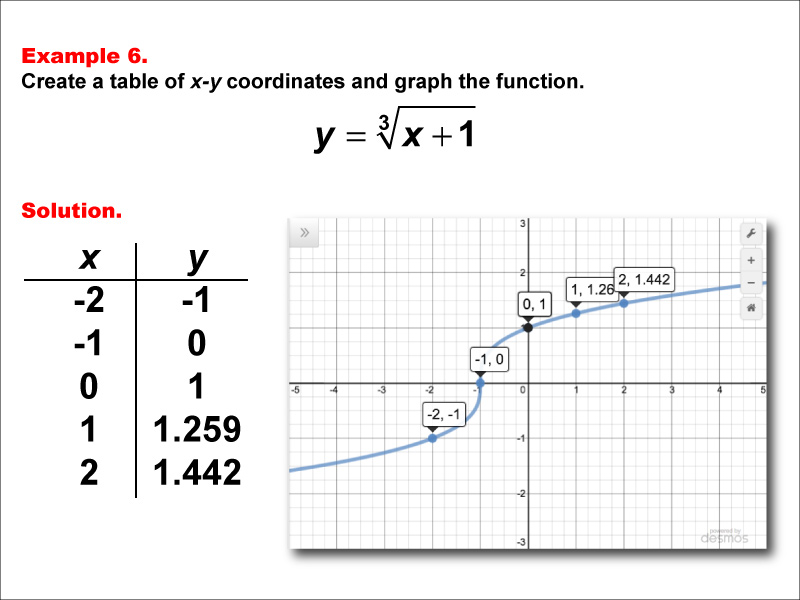
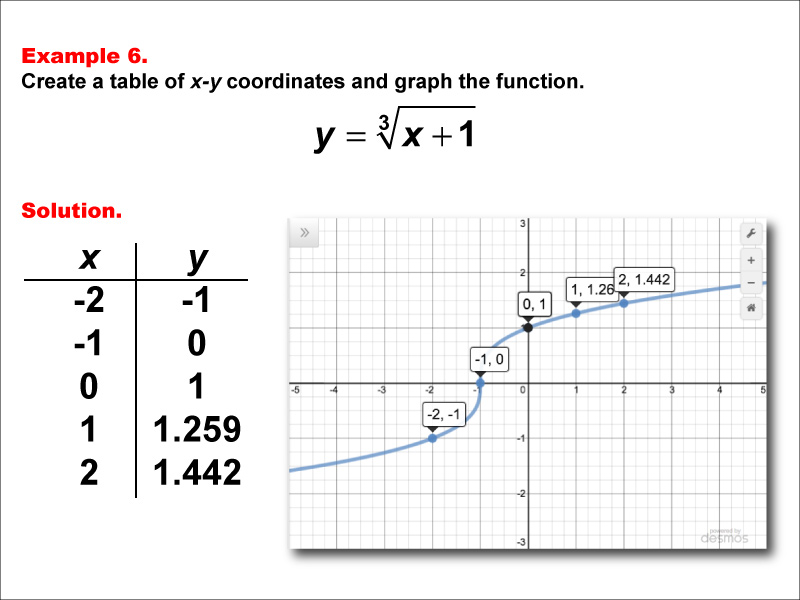
This example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = ∛(x + 1). The graph displays a curve with specific points plotted, including (-2, -1), (-1, 0), (0, 1), (1, 1.259), and (2, 1.442). This visual representation helps students understand how adding a constant term affects the cube root function.
Cube root functions are a crucial topic in advanced algebra and precalculus. They belong to the family of radical functions and exhibit unique properties that set them apart from other functions. This collection of examples provides a comprehensive look at various forms of cube root functions, helping students grasp their characteristics and behaviors under different transformations, including vertical shifts.
Offering multiple worked-out examples is essential for students to fully comprehend cube root functions. By examining different variations and transformations of these functions, students can develop a deeper intuition about their properties, such as their shape, domain, range, and how they respond to different transformations, including vertical translations.
Teacher's Script: Now, let's examine how adding a constant term affects the cube root function. How does adding 1 inside the cube root of x change the graph compared to y = ∛x? Notice how the entire curve is shifted left by 1 unit. Can you predict what would happen if we subtracted 1 instead? How would that affect the graph's position?
For a complete collection of math examples related to Cube Root Functions click on this link: Math Examples: Cube Root Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, cube root functions, graphs of cube root functions, cube root function tables |