Display Title
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 20
Display Title
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 20
Topic
Radical Functions
Description
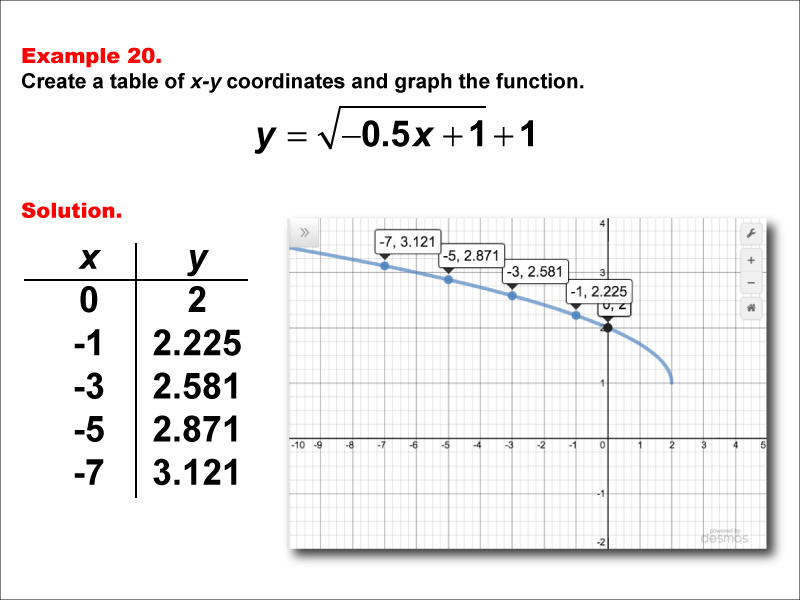
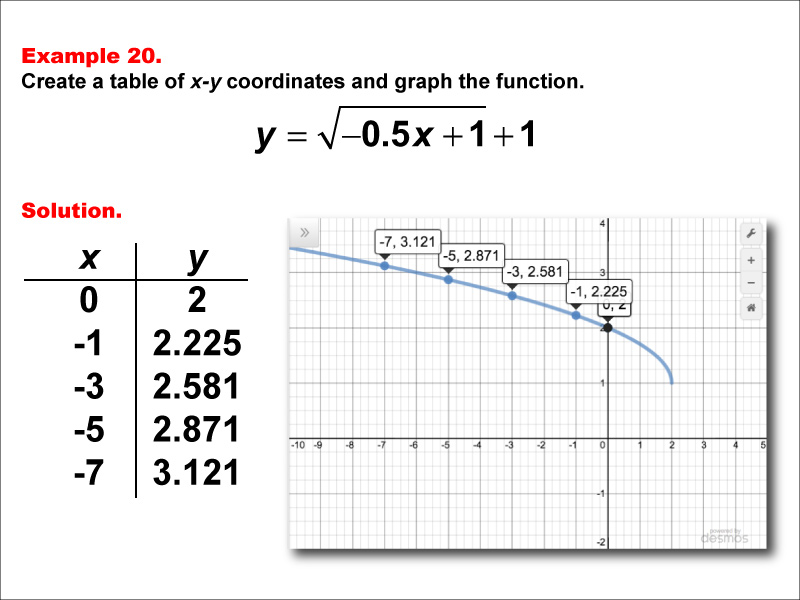
This example explores the function y = √(-0.5x + 1) + 1. The graph shows a decreasing curve starting at (0, 2) and moving downward as x becomes more negative. A table lists x-values (0, -1, -3, -5, -7) with corresponding y-values of 2, 2.225, 2.581, 2.871, and 3.121. Students are tasked with creating a table of x-y coordinates and graphing the function using these values.
This example combines concepts from previous examples, featuring a negative coefficient inside the radical, a fractional term, and constant terms inside and outside the radical. It helps students understand how these factors together affect the direction, steepness, domain, and vertical shift of the function. By comparing this to earlier examples, students can see how different elements of the equation influence the graph's behavior.
Presenting a variety of examples is crucial for building a comprehensive understanding of square root functions. Each new example challenges students to apply their knowledge in a slightly different context, reinforcing their learning and helping them develop problem-solving skills. This approach encourages students to think critically about the relationship between equations and their graphical representations.
Teacher's Script: Now, let's look at the function y = √(-0.5x + 1) + 1. How do you think this graph will compare to our previous examples? We'll create a table of x-y coordinates using non-positive x-values: 0, -1, -3, -5, and -7. What do you notice about the y-values? When we plot these points, we see that our curve is decreasing and only exists for non-positive x-values, similar to y = √(-2x + 1) + 1. However, it's rising more slowly and is shifted up by 1 unit. Can anyone explain why this is the case? How do the negative coefficient, the fraction inside the radical, and the constant terms affect the function's behavior?
For a complete collection of math examples related to Radical Functions click on this link: Math Examples: Square Root Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Radical Expressions and Functions • Radical Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, square root functions, graphs of square root functions, square root function tables |