Display Title
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 8
Display Title
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 8
Topic
Radical Functions
Description
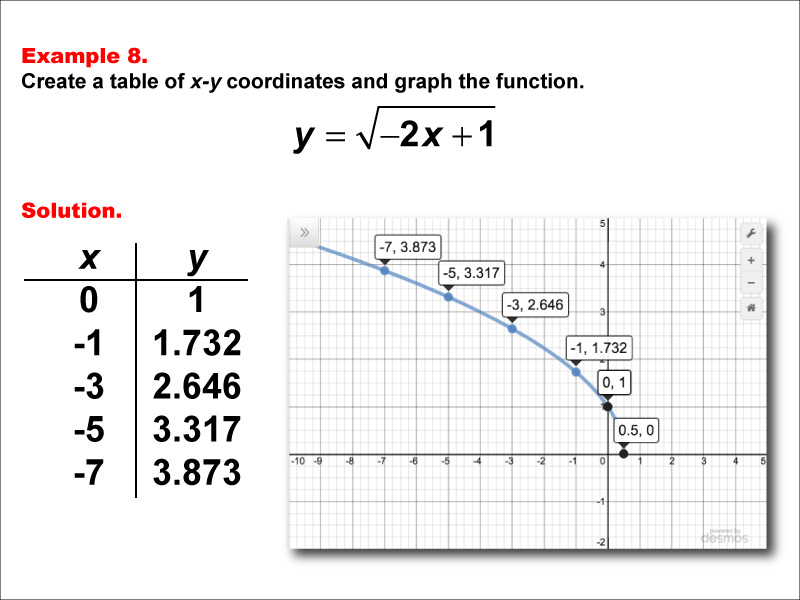
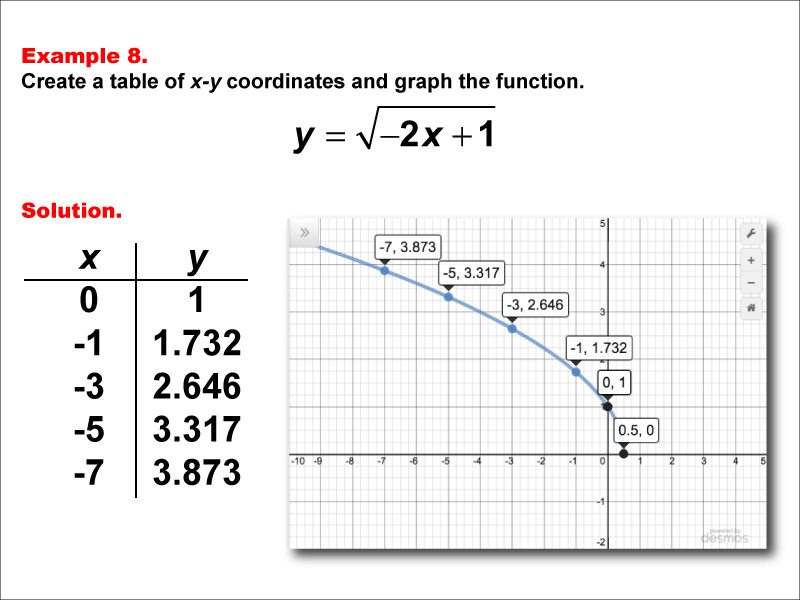
This example explores the function y = √(-2x + 1). The graph shows a decreasing curve starting at (0, 1) and moving downward as x decreases (negative values). A table lists x-values from -7 to 0 with their corresponding y-values, ranging from approximately 3.873 to 1. Students are tasked with creating a table of x-y coordinates and graphing the function y = √(-2x + 1), using x-values of 0, -1, -3, -5, -7 with corresponding y-values of 1, 1.732, 2.646, 3.317, and 3.873.
This example introduces students to square root functions with negative coefficients inside the radical, combined with a constant term. It helps them understand how these factors affect the direction, steepness, and domain of the function. By comparing this to previous examples, students can see how the graph is reflected and how the domain is restricted to x-values that make the expression under the square root non-negative.
Presenting a variety of examples is crucial for building a comprehensive understanding of square root functions. Each new example challenges students to apply their knowledge in a slightly different context, reinforcing their learning and helping them develop problem-solving skills. This approach encourages students to think critically about the relationship between equations and their graphical representations.
Teacher's Script: Now, let's look at the function y = √(-2x + 1). How do you think this graph will differ from our previous example? We'll create a table of x-y coordinates, but notice that we're using non-positive x-values this time: 0, -1, -3, -5, and -7. What happens to the y-values? When we plot these points, we see that our curve is decreasing and only exists for x-values less than or equal to 1/2. Can anyone explain why this is the case? How does the negative coefficient inside the square root affect the function's behavior?
For a complete collection of math examples related to Radical Functions click on this link: Math Examples: Square Root Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Radical Expressions and Functions • Radical Functions and Equations |
| Copyright Year | 2015 |
| Keywords | function, square root functions, graphs of square root functions, square root function tables |