Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 13
Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 13
Topic
Special Functions
Description
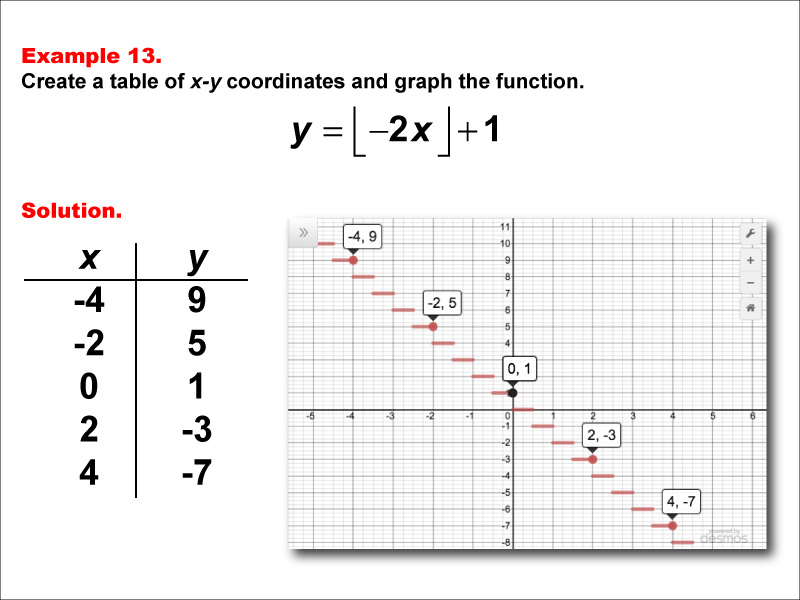
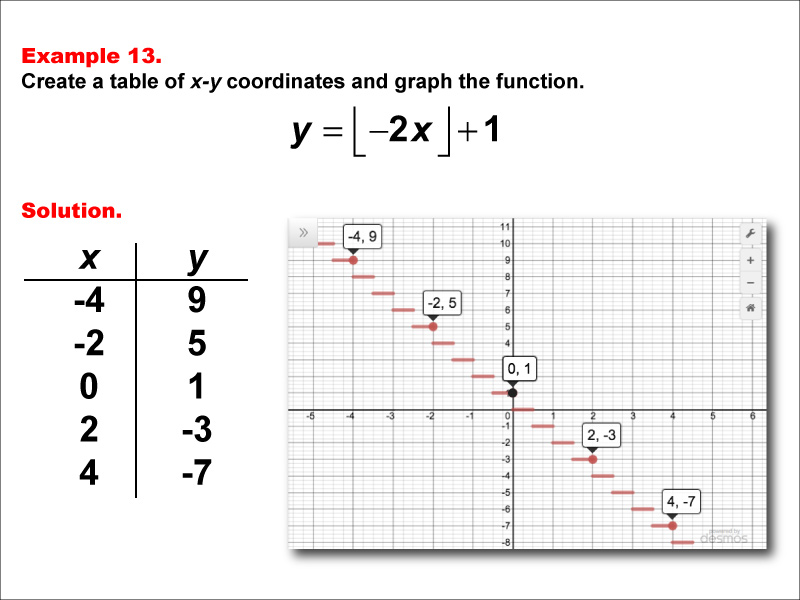
This example showcases a step function defined by y = floor(-2x) + 1. The graph features red horizontal segments and black points at key coordinates, with x values of -4, -2, 0, 2, and 4, and corresponding y values of 9, 5, 1, -3, and -7. This visual representation helps students understand how the function behaves across different intervals.
Step functions are a fundamental concept in mathematics, particularly in the study of special functions. This example aids in teaching the topic by providing a clear visual representation of how the floor function behaves when combined with a negative linear function and a constant. By examining both the table of coordinates and the corresponding graph, learners can develop a deeper understanding of how step functions behave and how modifications to the equation impact the resulting graph, especially the direction and frequency of the steps.
It is crucial for students to see multiple worked-out examples to fully grasp the concept of step functions. This example, along with others in the collection, highlights different aspects of these functions, such as varying coefficients or additional terms within the floor function. By exploring a range of examples, students can identify patterns, make connections, and build a more comprehensive understanding of step functions and their applications in real-world scenarios, such as in economics, computer science, and signal processing.
Teacher's Script: Let's examine the step function y = floor(-2x) + 1. Notice the red horizontal segments and black points on the graph. How do these visual elements help us understand the function's behavior? Compare this to our previous examples. What similarities and differences do you observe? Pay close attention to how the y-values change as x increases. As we continue through more examples, try to predict how changes in the coefficient of x and the constant outside the floor function will influence the graph's appearance, particularly the frequency, direction, and height of the steps.
For a complete collection of math examples related to Step Functions click on this link: Math Examples: Step Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Special Functions |
| Copyright Year | 2015 |
| Keywords | function, step functions, graphs of step functions, step function tables, greatest integer function |