Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 39
Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 39
Topic
Special Functions
Description
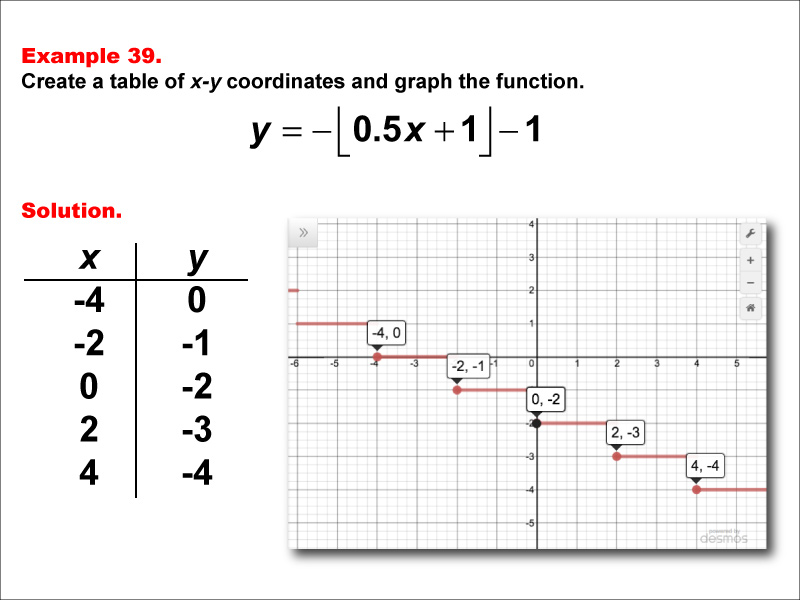
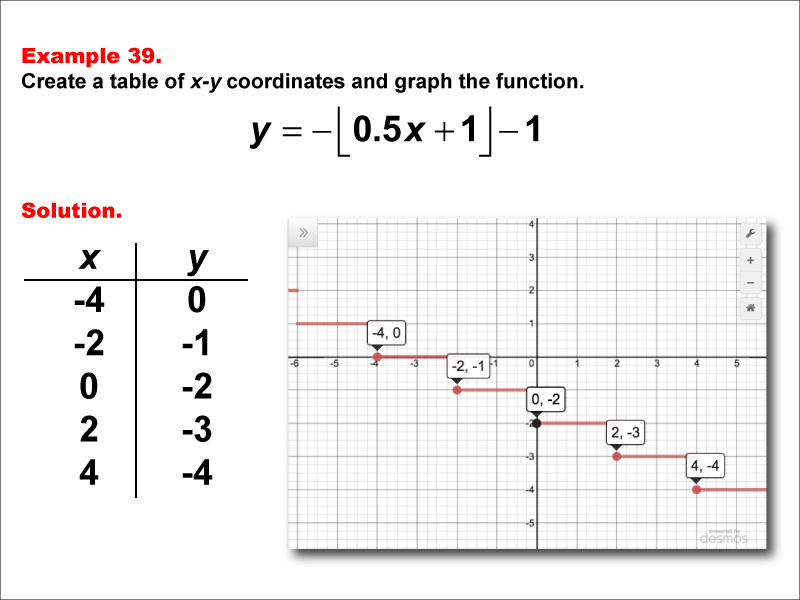
This example demonstrates a step function defined by y = -floor(0.5x + 1) - 1. The graph features horizontal steps at various points, with x-values from -4 to 4 and corresponding y-values of 0, -1, -2, -3, and -4. This visual representation helps students understand how multiplying x by a fraction inside the floor function, adding a constant, and then negating and subtracting outside affects the graph's appearance.
Step functions are a crucial concept in mathematics, particularly in the study of special functions. This example aids in teaching the topic by providing a clear visual representation of how complex modifications to the floor function, including fractional coefficients, impact the resulting graph. By examining both the table of coordinates and the corresponding graph, learners can develop a deeper understanding of how these modifications influence step functions.
It is essential for students to see multiple worked-out examples to fully grasp the concept of step functions. This example highlights different aspects of these functions, such as fractional coefficients, additional terms, and negation. By exploring a range of examples, students can identify patterns and build a more comprehensive understanding of step functions.
Teacher's Script: Now, let's examine y = -floor(0.5x + 1) - 1. Notice how using 0.5 as the coefficient of x affects the width of the steps compared to our previous examples. How does negating the entire floor function and subtracting one shift the graph? Pay close attention to how the y-values change as x increases. As we continue through more examples, try to predict how changes in the coefficient of x, especially when it's a fraction, will influence the graph's appearance, particularly the width of the steps and the range of y-values.
For a complete collection of math examples related to Step Functions click on this link: Math Examples: Step Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Special Functions |
| Copyright Year | 2015 |
| Keywords | function, step functions, graphs of step functions, step function tables, greatest integer function |