Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 6
Display Title
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 6
Topic
Special Functions
Description
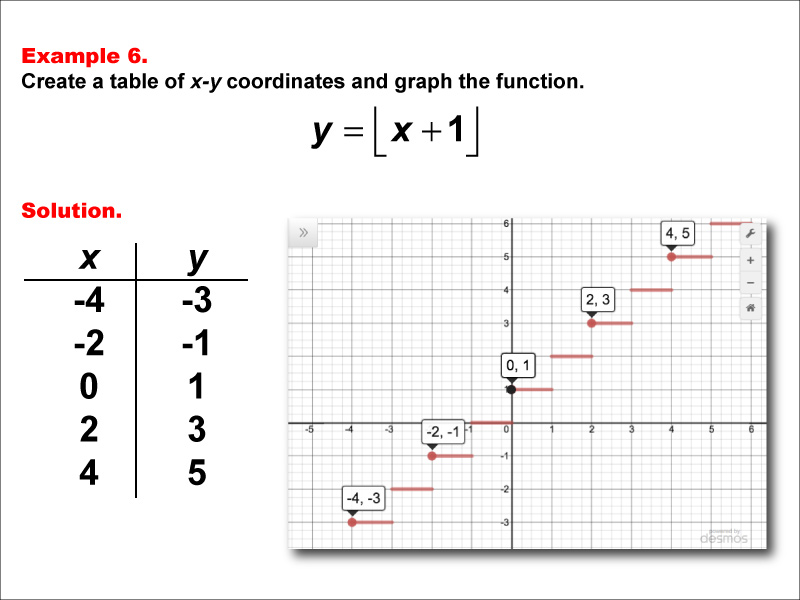
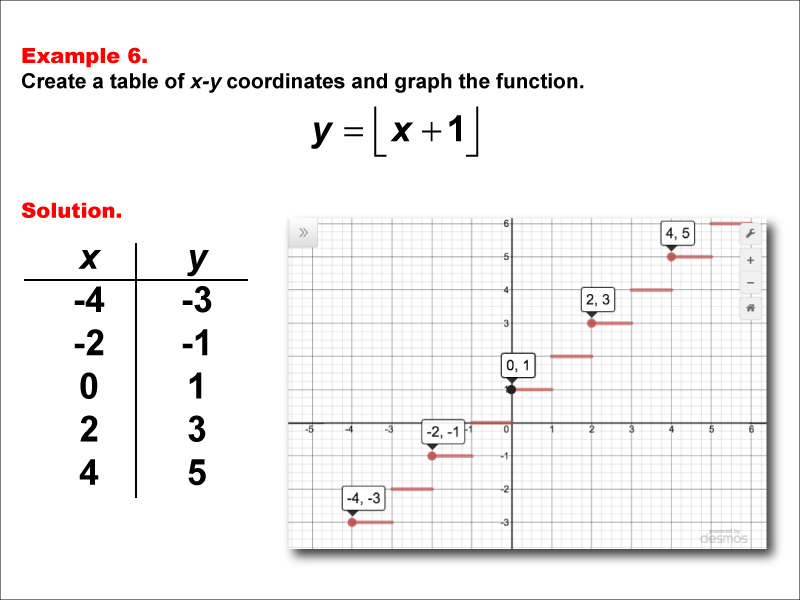
This example demonstrates a step function defined by y = floor(x + 1). The table includes x-values (-4, -2, 0, 2, 4) and corresponding y-values (-3, -1, 1, 3, 5). The graph illustrates how this function behaves, with distinct horizontal segments that show the "stepping" nature of the function. This example helps students visualize how adding 1 to x inside the floor function affects the graph's appearance, particularly the vertical shift of the steps.
Step functions are a crucial concept in mathematics, especially in the study of special functions. This collection of examples aids in teaching the topic by providing visual representations of various step functions, allowing students to observe how different equations translate into graphical form. By examining both the table of coordinates and the corresponding graph, learners can develop a deeper understanding of how step functions behave and how modifications to the equation impact the resulting graph, including vertical shifts and changes in the y-intercept.
Exposure to multiple worked-out examples is essential for students to fully comprehend the concept of step functions. Each example in this collection highlights different aspects of these functions, such as varying coefficients, additional terms, or transformations within the floor function. By exploring a range of examples, students can identify patterns, make connections, and build a more comprehensive understanding of step functions and their applications in real-world scenarios, such as in computer programming, data analysis, and modeling discrete phenomena.
Teacher's Script: Now, let's look at our sixth example, y = floor(x + 1). Compare this to our previous examples, especially the first one. What do you notice about the position of the steps? How has adding 1 to x inside the floor function affected the graph? Pay attention to how the y-values change compared to the original function y = floor(x). As we continue through more examples, try to predict how adding or subtracting constants inside the floor function will influence the graph's appearance, particularly the vertical positioning of the steps.
For a complete collection of math examples related to Step Functions click on this link: Math Examples: Step Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Special Functions |
| Copyright Year | 2015 |
| Keywords | function, step functions, graphs of step functions, step function tables, greatest integer function |