Display Title
Math Example--Volume Concepts--Calculating Volume: Example 16
Display Title
Math Example--Volume Concepts--Calculating Volume: Example 16
Topic
Volume
Description
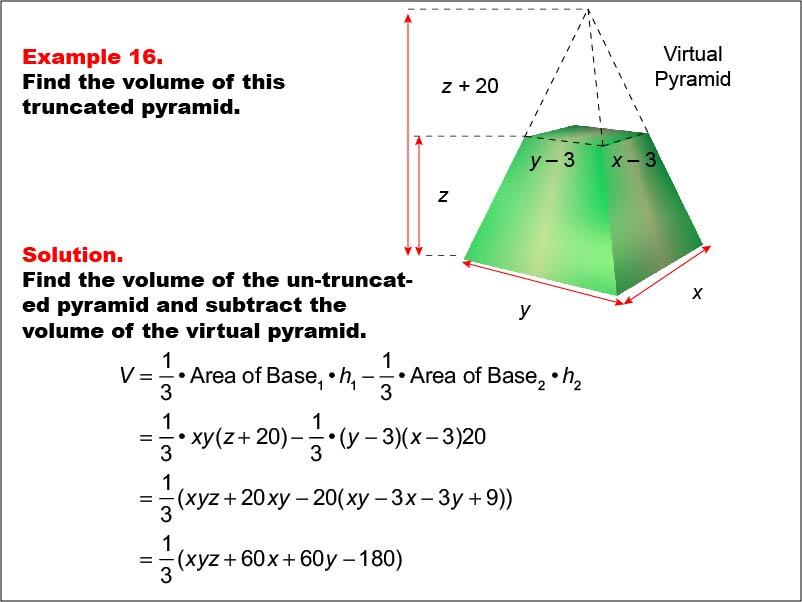
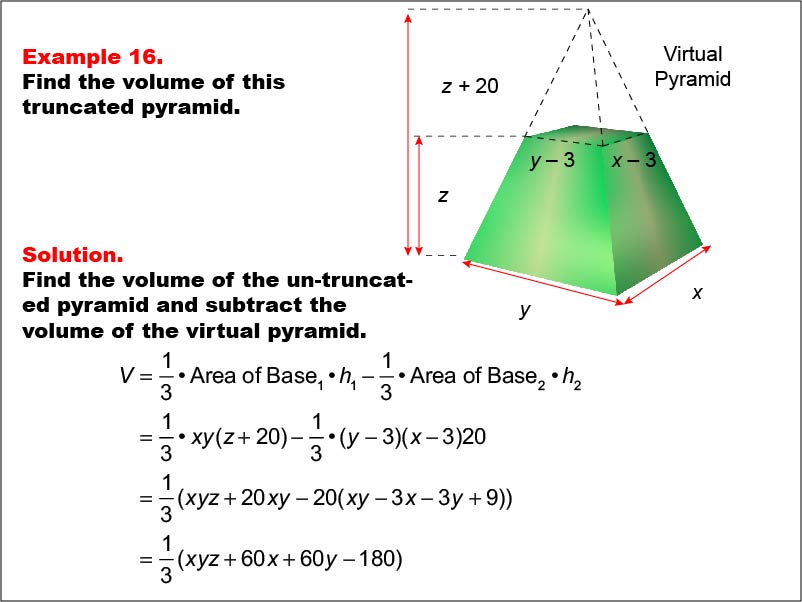
A truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180).
Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes.
Seeing multiple worked-out examples allows students to observe different approaches and nuances in calculations, which reinforces their understanding of volume across shapes.
Teacher's Script: Observe this example carefully. Notice the steps taken to find the volume of this particular shape. Can you see how each dimension--length, width, and height--plays a role in determining the overall volume? How might you apply this to other shapes?
For a complete collection of math examples related to Volume click on this link: Math Examples: Volume Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.G.A.2, CCSS.MATH.CONTENT.7.G.B.6, CCSS.MATH.CONTENT.8.G.C.9, CCSS.MATH.CONTENT.5.MD.C.4, CCSS.MATH.CONTENT.5.MD.C.5.A, CCSS.MATH.CONTENT.5.MD.C.5.B, CCSS.MATH.CONTENT.5.MD.C.5.C |
|---|---|
| Grade Range | 5 - 8 |
| Curriculum Nodes |
Geometry • Surface Area and Volume • Volume |
| Copyright Year | 2013 |
| Keywords | volume |