Display Title
Video Definition 14--3D Geometry--Horizontal Cross-Section of a Cylinder
Display Title
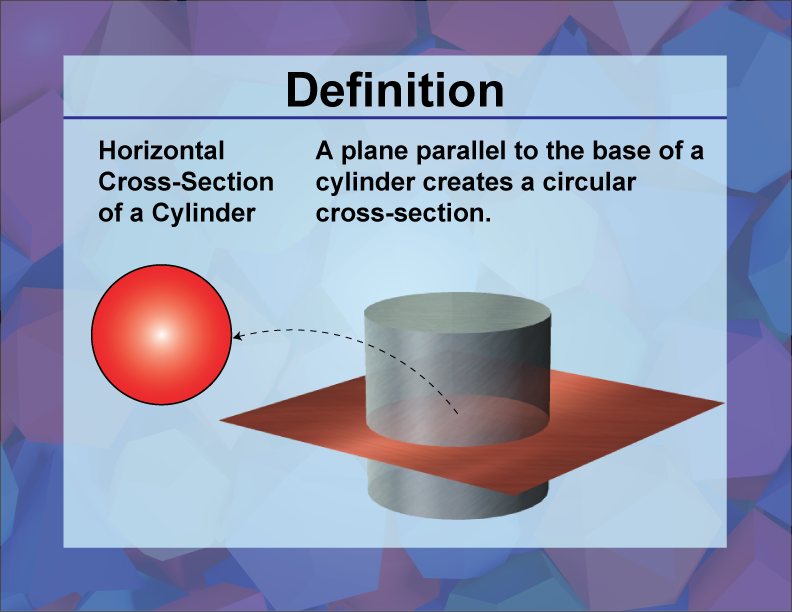
Horizontal Cross-Section of a Cylinder
Topic
3D Geometry
Definition
A horizontal cross-section of a cylinder is the intersection of the cylinder with a horizontal plane, resulting in a circle.
Description
Horizontal cross-sections of a cylinder are important for understanding cylindrical geometry. When a cylinder is sliced horizontally, the resulting shape is a circle, which is crucial for calculating properties like volume and surface area. This concept is applied in fields like engineering and manufacturing, where precise measurements are needed for cylindrical components. In math education, studying cross-sections of cylinders helps students grasp the concept of symmetry and the properties of circles in three-dimensional space. For example, a horizontal cross-section of a cylinder at its midpoint results in a circle with the same radius as the cylinder's base.

For a complete collection of terms related to 3D Geometry click on this link: 3D Geometry Video Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3, CCSS.MATH.CONTENT.7.G.A.3 |
|---|---|
| Duration | 1 minutes |
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • Cylinders |
| Copyright Year | 2024 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term, cylinder |