Display Title
Video Definition 18--3D Geometry--Horizontal Cross-Section of a Tetrahedron
Display Title
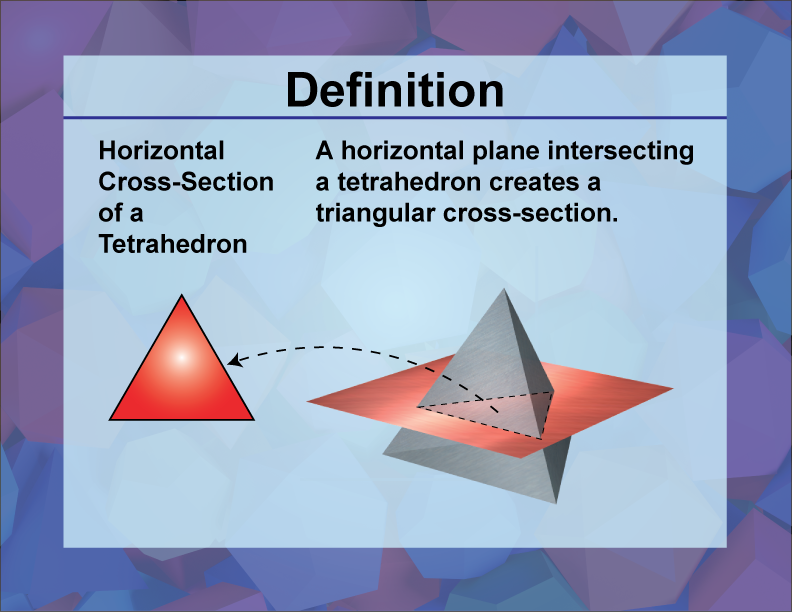
Horizontal Cross-Section of a Tetrahedron
Topic
3D Geometry
Definition
A horizontal cross-section of a tetrahedron is the intersection of the tetrahedron with a horizontal plane, resulting in a triangle or another polygon.
Description
Horizontal cross-sections of a tetrahedron provide insights into the tetrahedron's internal structure. Depending on the plane's position, the resulting shape can be a triangle or another polygon, illustrating the relationship between the tetrahedron's faces and its apex. This concept is useful in fields like architecture and design, where tetrahedral shapes are used to create innovative structures. In math education, studying cross-sections of tetrahedrons helps students understand the relationship between two-dimensional and three-dimensional geometry, enhancing their spatial reasoning skills. For example, a horizontal cross-section of a tetrahedron at its midpoint results in a smaller triangle, illustrating the tetrahedron's symmetry.

For a complete collection of terms related to 3D Geometry click on this link: 3D Geometry Video Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Duration | 1 minutes |
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • 3-Dimensional Figures |
| Copyright Year | 2024 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |