Display Title
Video Definition 22--Rationals and Radicals--Oblique Asymptote
Display Title
Video Definition 22--Rationals and Radicals--Oblique Asymptote
Topic
Rationals and Radicals
Description
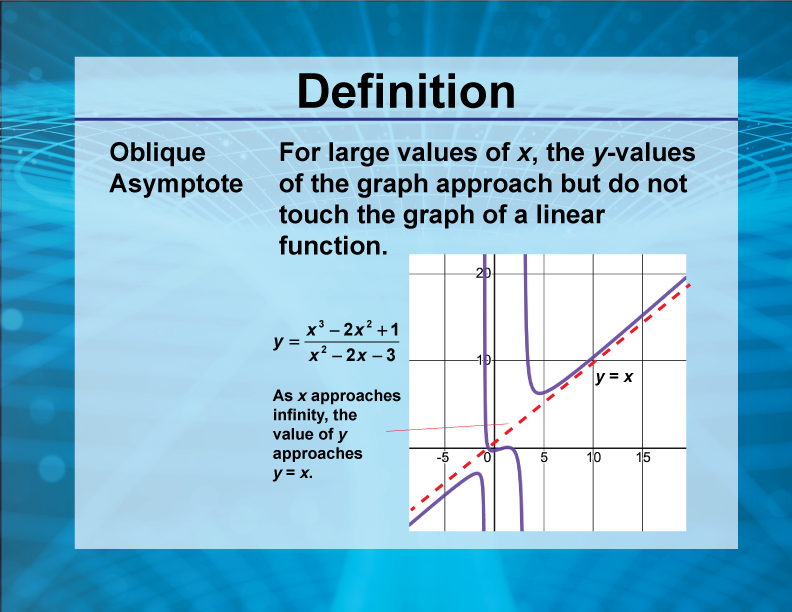
An oblique asymptote occurs when, for large values of x, the y-values of the graph approach but do not touch the graph of a linear function. An example is given where y = (x3 - 2x2 + 1) / (x2 - 2x - 3) approaches y = x as x approaches infinity. This term provides insight into the behavior of rational functions, essential for graphing and understanding limits in radical and rational contexts.
Understanding this video is essential for grasping the fundamentals of Rationals and Radicals. The mathematical concepts explored here form the basis for further exploration and application in related fields.
Teacher's Script: "Today, we will delve into an important concept that helps us simplify and solve complex problems in mathematics. This video introduces the concept of an Oblique Asymptote and shows how it applies in various scenarios. Pay close attention to how the examples are worked out."
For a complete collection of videos related to Rationals and Radicals click on this link: Math Video Definitions: Rationals and Radicals Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.A.2, CCSS.MATH.CONTENT.HSN.RN.A.1, CCSS.MATH.CONTENT.HSF.IF.C.7 |
|---|---|
| Duration | 1 minutes |
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2024 |
| Keywords | radicals, radical expressions, rational numbers, rational expressions, definitions, glossary term, rational functions |