
Display Title
Video Tutorial: Algebra Tiles 17
Display Title
Video Tutorial: Algebra Tiles 17
Topic
Expressions and Equations
Description
This video explains solving one-step equations like x + 2 = 4 and x ÷ 2 = 4 with algebra tiles. It covers addition, subtraction, multiplication, and division operations. Key vocabulary includes one-step equations, zero pairs, and operations.
Relevance: This video ties into the topic of Expressions and Equations by providing students with a hands-on approach to understanding the concepts of algebra. Algebra tiles serve as a visual and tactile way to model mathematical operations, helping students internalize these ideas effectively.
Mathematics Behind the Topic: The video delves into the mathematical principles behind the use of algebra tiles. For example, students learn to represent positive and negative values using specific tiles and to simplify expressions using zero pairs. This tactile method makes abstract algebraic concepts concrete and accessible.
Teacher's Script: "Class, today we are diving into a hands-on approach to understanding algebra. This method uses algebra tiles, which are visual tools that help represent mathematical operations. As you watch, think about how these tiles can simplify expressions or model equations. Pay close attention to how positive and negative tiles interact, especially when forming zero pairs. These ideas will form the basis of what we practice in class today."
For a complete collection of videos related to Expressions and Equations click on this link: Video Tutorials: Algebra Tiles Collection.
What Are Algebra Tiles?
Algebra Tiles are a very useful numerical model for positive integers, negative integers, and even variables. Algebra tiles usually come in three main colors: red, yellow, and green.
- The red tiles model negative numbers.
- The yellow tiles model positive numbers.
- Green tiles model unknown quantities, such as the variable x.
Each tile represents a quantity. For example, one red tile represents -1 and two yellow tiles represent +2.
Modeling Integers Using Algebra Tiles
The set of integers includes zero, positive whole numbers, and negative whole numbers. Integers are represented by this set:
{...-3, -2, -1, 0, 1, 2, 3...}
Algebra tiles are very useful for modeling integers. This is especially useful when first introducing the idea of negative numbers. The red and yellow tiles clearly demonstrate that these are different types of numbers.
Here are examples of modeling positive integers using algebra tiles. The number of tiles represents the numerical value of the integer.
Here are examples of modeling negative integers using algebra tiles. Once again, make a note of the number of tiles and the number that they represent.
Modeling Zero
You can even model zero by placing a positive tile and a negative tile next to each other. This is called a zero pair. By placing one yellow tile next to one red tile, they form a zero pair because of the following fact:
1 + (-1) = 0
There are even multiple ways of modeling zero, so long as equal numbers of red and yellow tiles are used.
Why is it necessary to model zero using algebra tiles? As you'll see, when it comes to solving equations using algebra tiles, creating zero pairs is an important part of the process.
Adding Integers Using Algebra Tiles
When you're working with number models, you can also model basic operations. Here we look at adding and subtracting integers using algebra tiles.
If you're adding two positive integers, you can use algebra tiles to model the sum. Here's an example. Notice that the sum is positive.
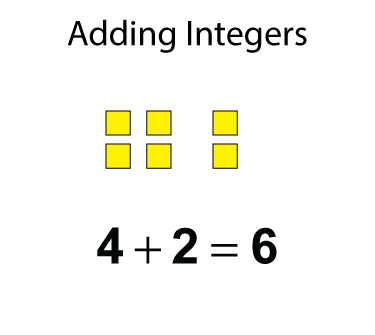
The same idea applies to adding two negative integers. Take a look at this example. Notice that the sum is negative.

When you're adding integers that are a mix of positive and negative numbers, use an algebra tiles model to form zero pairs to find the sum. Here is an example.
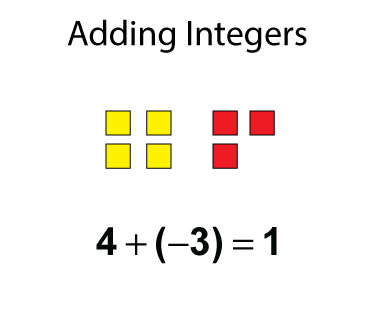
Subtracting Integers Using Algebra Tiles
Modeling subtraction with algebra tiles involves the familiar "take away" model. Here's a simple example. Start with the algebra tiles and then take away the number needed. What's left is the difference.
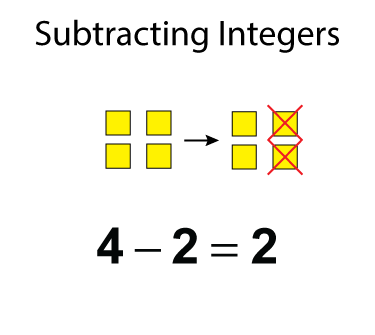
In this example, we have four positive tiles and want to take two away. Since there are four tiles there, then taking two away leaves two tiles.
But what if there are no tiles to "take away"? For example, how would you use algebra tiles to model this subtraction expression?
4 – (-2)
If there are four positive tiles (yellow), how can we take away two negative tiles (red)? This is where you use zero pairs. Look at this example.
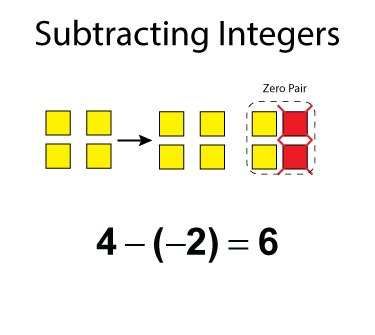
We start with four yellow tiles (+4), but we can't take away any red tiles. So, add a zero pair that includes two red tiles. Notice the zero pair on the right. Now take away the red tiles and what's left over (+6) is the difference.
Modeling Expressions
An algebraic expression includes a variable and a number. Here is an example of an algebraic expression:
x + 4
Algebra tiles can also be used to model algebraic expressions. To model such expressions, use the tall green tile to model the variable. Take a look at these examples. Make a note of the type of algebra tile used and its color.
Modeling Equations
When an algebraic expression equals a number, then an equation is formed. Here's such an equation.
x + 2 = 1
You can also use algebra tiles to model and solve equations.
This is where zero pairs come into play when solving equations. Use zero pairs to solve for the variable. In the equation shown above, add two red tiles to both sides of the equation to cancel out the two yellow tiles on the left. The result is shown below.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.B.5, CCSS.MATH.CONTENT.7.EE.B.3, CCSS.MATH.CONTENT.7.EE.B.3, CCSS.MATH.CONTENT.8.EE.C.7.A, CCSS.MATH.CONTENT.8.EE.C.7.B |
|---|---|
| Duration | 12.00 minutes |
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Algebra Tiles--Expressions and Equations |
| Copyright Year | 2016 |
| Keywords | algebra tiles, solving equations, video tutorial |