
Display Title
Video Tutorial: Rational Numbers: Video 2
Display Title
Video Tutorial: Rational Numbers: Video 2
Topic
Rational Numbers
Description
The video explores rational and irrational numbers. Rational numbers include integers, fractions, and repeating decimals. Irrational numbers, such as the square root of non-perfect squares and pi, are non-terminating and non-repeating. Examples include Pythagorean triples and circle circumference ratios. Applications focus on distinguishing between the two.
The relevance of this video to the topic of Rational Numbers lies in its ability to visually and interactively demonstrate key mathematical concepts. Rational numbers are fundamental for understanding how numbers can be expressed as fractions, decimals, and ratios. The video uses clear examples and practical applications to help solidify these mathematical principles.
Teacher's Script: "Today, we are diving into a fascinating part of mathematics: rational numbers. This video introduces rational numbers, defined as ratios of two integers where the denominator is non-zero. Notice how the examples in the video highlight practical ways to represent and compare rational numbers. As you watch, think about how these ideas connect to our previous lessons and how you can apply them in solving problems."
For a complete collection of videos related to Rational Numbers click on this link: Video Tutorials: Rational Numbers Collection.
A Brief Review of Integers
Before defining rational numbers, we first need to review integers. The definition of a rational number involves integers, so let's make sure you're comfortable with the definition of integers.
Integers include the whole numbers, zero, and positive numbers 1, 2, 3, etc., but also includes a different class of numbers, negative numbers.
You can use a number line to represent the integers.
Notice that every integer and its opposite is the same distance from 0 on the number line. Also, the arrow heads on the number line mean that the integers extend to infinity.
Notice that every integer and its opposite is the same distance from 0 on the number line. Also, the arrow heads on the number line mean that the integers extend to infinity.
Representing distance on a number line is shown below.

Distance is always a positive number, so use the absolute value symbol to ensure the result is positive. Subtract one value from another and find the absolute value of the difference.
Every integer has its opposite. Notice on the number line that 1 and -1 are opposites, as are 2 and -2, and so on. Every integer and its opposite is the same distance from zero on the number line, as shown below.
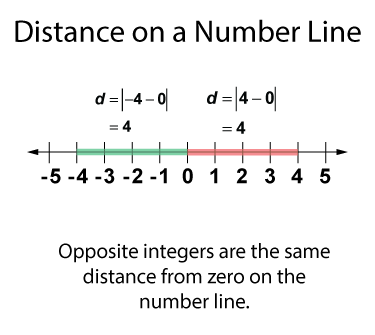
As you can see both 4 and -4 are four units from zero. This same pattern applies to all integers and their opposites. Also, the sum of any integer and its opposite is zero.
1 + (-1) = 0
2 + (-2) = 0
This pattern continues for all integers and their opposites.
The technique of finding the absolute value of a difference applies to any pair of integers, as shown below.

Defining Rational Numbers
All rational numbers can be written as shown below. A rational number looks like a fraction, but it is a ratio of two numbers. As with fractions, the denominator cannot be zero.
Rational numbers can be written in different ways.
Integers are examples of rational numbers.
If a number cannot be written as the ratio of two integers, then it is an irrational number.
Rational numbers can be graphed on a number line. Make a note of the rational numbers in decimal form graphed on the number line below. However, keep in mind that the integer values are also rational numbers.
Rational numbers and their opposites, as with integers, add up to zero. Every rational number has its opposite.
Adding and Subtracting Rational Numbers
Add and subtract rational numbers the way you would add fractions. Here is an example of combining a positive and negative rational number.
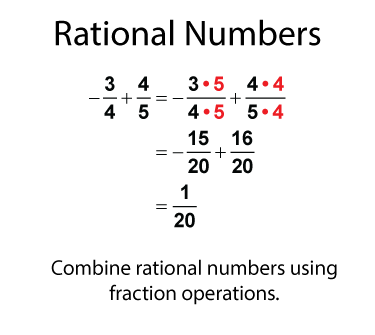
Here is another example. In this example the result is a negative number.
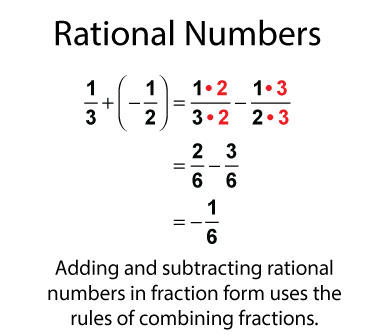
Adding and subtracting rational numbers in fraction form is a lot like adding and subtraction fractions. The main difference is that these fractions can be negative.
When expressed as decimals, combine rational numbers the way you would decimals.
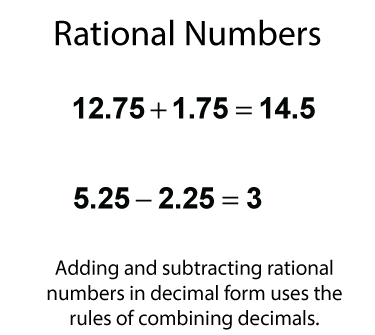
Adding and subtracting rational numbers in decimal form is a lot like adding and subtraction decimals. The main difference is that these decimals can be negative.
Multiplying Rational Numbers
Multiply rational numbers the way you would multiply fractions. Here are examples of multiplying rational numbers. The second example shows how to divide out common factors before multiplying.
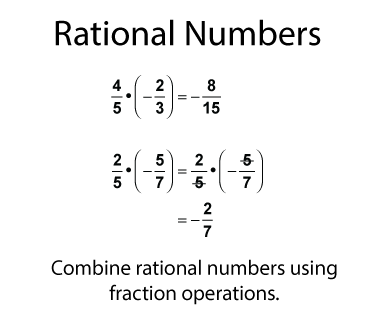
Multiplying rational numbers in fraction form is a lot like multiplying fractions. The main difference is that these fractions can be negative.
Rational Expressions
Rational numbers are ratios of two integers. Similarly, a rational expression is the ratio of two algebraic expressions. The algebraic expression can be a number or a polynomial. Here are three examples of rational expressions.
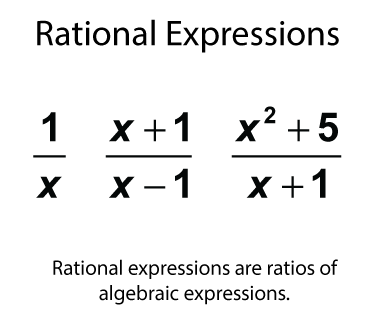
Like rational numbers, the denominator can't be zero. Let's see what that looks like for the expressions above.
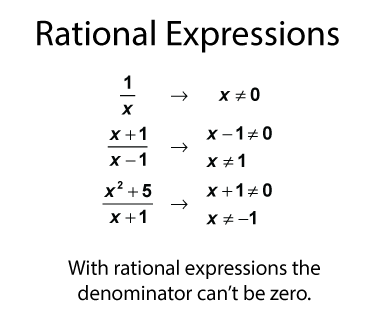
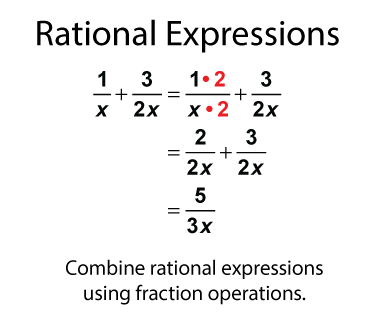
Like rational numbers, rational expressions can be combined. Use fraction operations to combine rational expressions.
Simplify rational expressions by finding common factors in the numerator and denominator. In this example there is a common term, x + 1, that divides out of both the numerator and denominator.
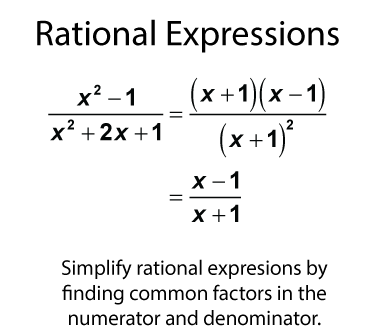
Rational Equations
When a rational expression equals a number, this forms a rational equation, which can be solved for the variable. Here is an example of a rational equation and its solution.
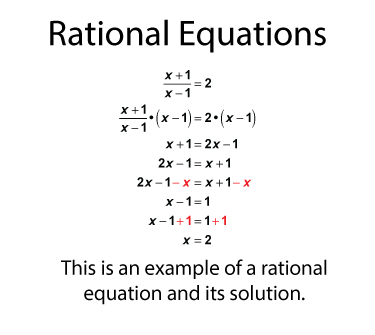
| Common Core Standards | CCSS.MATH.CONTENT.6.RP.A.1, CCSS.MATH.CONTENT.7.NS.A.2.A, CCSS.MATH.CONTENT.8.NS.A.1, CCSS.MATH.CONTENT.6.NS.C.5, CCSS.MATH.CONTENT.6.NS.C.6, CCSS.Math.CONTENT.7.NS.A.1, CCSS.MATH.CONTENT.7.NS.A.1.C, CCSS.MATH.CONTENT.7.NS.A.1.D, CCSS.MATH.CONTENT.8.NS.A.1, CCSS.MATH.CONTENT.8.NS.A.2, CCSS.MATH.CONTENT.HSN.RN.B.3 |
|---|---|
| Duration | 5.00 minutes |
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Expressions |
| Copyright Year | 2017 |
| Keywords | rational numbers, rational numbers video tutorials, video tutorials, irrationals, video tutorial |