Video Tutorial: Slope Formula: Negative Slope, Coordinates in Quadrant II

This is part of a collection of video tutorials on the topic of the Slope Formula. These videos cover ways of calculating slope, as well as positive, negative, zero, and undefined slope.

—CLICK PREVIEW TO SEE THE VIDEO TUTORIAL—

To see the complete collection of the video tutorials on this topic, click on this link.

The following section includes background information on the slope formula. Refer to this as you review all the videos in the collection.

What Is Slope?

Slope is a surprisingly complicated concept. Slope involves these components.

• A ratio of two measurements
• The measurements are coordinate differences
• The coordinate differences are based on the coordinates of two points in an x-y Cartesian coordinate system

So, let's look at the two main ideas separately: ratios and Cartesian coordinates.

Brief Review of Ratio

What is a ratio? It is a relationship between two quantities. Take a look at the definition.

Click on this link to learn more about ratios. This slide show includes a video and examples of different ratios. Here are some additional ratios topics you should review. Each of the following includes a link to a slide show with additional content:

• Ratios with Three Items: Explore ratios of the form a:b:c.
• Ratios with Fractions: Explore ratios where the the terms are made up of fractions.
• Equivalent Ratios: Explore ratios that represent the same amount.

Calculating Slope Without Coordinates

Slope is a ratio. So, before we review the coordinates component, we can begin calculating slope now.

Take a look at this right triangle. 

You can see that we know the vertical height of the triangle (also called the rise) and the horizontal length (also called the run), so we have all the information he need to calculate the slope. The equation shown results in a slope of 3/4. 

But for this right triangle, what is the slope a measurement of? This right triangle has horizontal and vertical lengths. The slope is a measure of the orientation of the third side of the triangle.

So, you don't need coordinates to calculate slope. In fact, when calculating the pitch of a roof (an equivalent to the slope) vertical and horizontal measurements are often used. For example, take a look at this illustration of a roof. Note the orange triangle, which can be used to calculate the pitch of the roof.

Suppose that the height of the overlaid triangle is 9 feet and the horizontal distance is 18 feet. The pitch of this slope is shown below.

Rise : Run

9 : 18

This can be simplified as a ratio of 1:2.

Although slope can be calculated as a ratio without coordinate measurements, the slope formula is often written as a ratio that involves coordinates. So, now we review Cartesian coordinates.

Brief Review of Cartesian Coordinates

Slope is the ratio of the difference in coordinates. Let’s briefly review the Cartesian coordinate system.

The Cartesian coordinate system consists of two axes that are perpendicular to each other. The horizontal axis is labeled x and the vertical axis is labeled y.

Each axis is a number line that represents all positive and negative real numbers, as well as zero. There are four quadrants, which are labeled as shown. 

A point on this coordinate grid has coordinates x and y, as shown below.

With this as the background, let's now look at how to calculate slope using coordinates. 

Slope

As we have noted, slope is a ratio. See the formal definition below, which includes the ratio of the rise over the run.

Recall that a ratio can look like a fraction and can be thought of as one number divided by another. What two numbers make up this ratio? As you can see from the definition, it’s the ratio of the change in y-coordinates over the change in x-coordinates.

Where do these changes in coordinates come from? Take a look at this example. There are two points, each with its own coordinates. For this example, we label the coordinates as variables, instead of numbers.

The difference in the y-coordinates is shown in this equation:

The difference in the x-coordinates is shown in this equation:

The ratio of these differences is shown below:

This ratio is also known as the slope formula.

Slope can be positive, negative, zero, or even be undefined. This illustration summarizes the four main types of slope measurements.

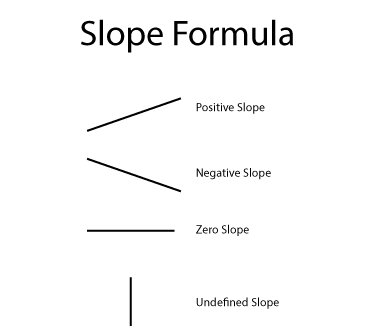
When the orientation of a line goes up in going from left to right, then it has a positive slope. When the orientation of a line goes down in going from left to right, then it has a negative slope. A horizontal line has a slope of zero. A vertical line has an undefined slope because in the slope formula it would involve dividing by zero, which is what makes the slope undefined.

Note: The download is an MP4 video file.

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Video Library

To see the complete collection of math videos, click on this link.

Closed Captioned Video Library

This video is available in closed captioned format. To see the complete collection of captioned videos, click on this link.

Video Transcripts

This video has a transcript available. To see the complete collection of video transcripts, click on this link.