Lesson Plan: Linear Inequalities

Lesson Objectives

Understand the concept of linear inequalities
Graph linear inequalities on the coordinate plane
Solve linear inequalities algebraically
Interpret and apply linear inequalities in real-world situations

Common Core Standards

6.NS.C.7a: Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram.
6.EE.B.5: Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
8.EE.B.5: Graph proportional relationships, interpreting the unit rate as the slope of the graph.
8.EE.C.7b: Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.

Prerequisite Skills

Understanding of linear equations
Graphing linear equations
Solving linear equations algebraically

Key Vocabulary

Linear inequality
Solution set
Inequality symbol (≤, ≥, <, >)
Boundary line

Warm-up Activity (10 minutes)

Introduce the concept of inequalities by asking students to compare two quantities using inequality symbols (e.g., 5 < 7, 10 ≥ 8). Discuss how inequalities are different from equations and how they represent a range of values rather than a single value.

Use this slide show to go over math examples of inequalities in one variable graphed on a number line:

https://www.media4math.com/library/slideshow/math-examples-one-variable-inequalities

Teach (20 minutes)

Introduction to Linear Inequalities

Use this slide show to review these definitions of inequalities:

https://www.media4math.com/library/slideshow/definitions-inequalities

Provide examples of linear inequalities and discuss their meaning (e.g., 2x + 3 ≤ 7 means that the value of 2x + 3 must be less than or equal to 7).

Graphing Linear Inequalities

Demonstrate how to graph a linear inequality on the coordinate plane by graphing the boundary line and shading the appropriate region. Emphasize the importance of the inequality symbol in determining which region to shade.

Use this selection of clip art images to show the contrast between equations and inequalities with one and two variables:

https://www.media4math.com/library/75525/asset-preview

Use this Desmos activity to explore graphs of linear inequalities:

https://www.desmos.com/calculator/vhqsry1h6b

Use this slide show to look at examples of graphs of linear inequalities:

https://www.media4math.com/library/slideshow/math-examples-linear-inequalities

Solving Linear Inequalities Algebraically

Introduce the process of solving linear inequalities algebraically, similar to solving linear equations. Emphasize the importance of reversing the inequality symbol when multiplying or dividing by a negative number.

Use this slide show to demonstrate how to solve one-step inequalities algebraically:

https://www.media4math.com/library/slideshow/solving-one-step-inequalities

Use this set of math clip art images to demonstrate how to solve linear inequalities:

https://www.media4math.com/library/75527/asset-preview

Review (5 minutes)

Review the key concepts covered in the lesson, including the definition of linear inequalities, graphing linear inequalities, and solving linear inequalities algebraically.

Use this video to see an application of linear inequalities in the context of business:

https://www.media4math.com/library/39668/asset-preview

The first few minutes of this video sets up the scenario and you will see the resulting inequality:

y > -2/3x + 20

While the video shows how to graph this inequality on a TI-Nspire graphing calculator, you can also use Desmos.

Assess (10 minutes)

Quiz

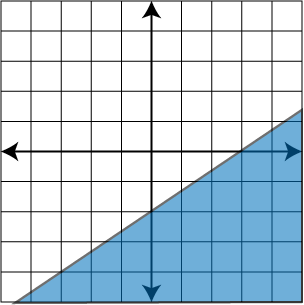
Graph the linear inequality: 2x - 3y ≥ 6
Solve the linear inequality: 4x + 2y < 10
Which of the following points does not satisfy the inequality 3x - 2y ≤ 12?
a) (2, 3)
b) (5, 1)
c) (1, 4)
d) (3, 2)
Write an inequality to represent the situation: The cost of a movie ticket is \$8 for adults and \$6 for children, and you have \$50 to spend. What combination of tickets can you purchase?
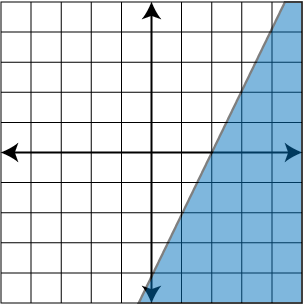
Graph the linear inequality: y ≥ 2x - 4
Which of the following points does not satisfy the inequality 2x + y ≤ 6?
a) (1, 2)
b) (2, 0)
c) (0, 4)
d) (3, 1)