Lesson Plan: Representing Proportional Relationships

Lesson Objectives

This lesson can be completed in one 50-minute class period. However, additional practice may be beneficial and could extend into a second class period if time allows.

• Represent proportional relationships using equations
• Graph proportional relationships
• Interpret points on graphs of proportional relationships, particularly (0, 0) and (1, r)
• Explain the meaning of points on graphs in real-world contexts
• Solve proportions using equations and ratio tables

Common Core Standards

7.RP.A.2c Represent proportional relationships by equations.

7.RP.A.2d Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.

Prerequisite Skills

• Understanding of proportional relationships
• Basic algebraic concepts
• Familiarity with coordinate plane
• Ability to interpret ratios and unit rates

Key Vocabulary

• Equation
• Coordinate plane
• y-intercept
• Slope
• Unit rate
• Proportional relationship

Warm-up Activity (10 minutes)

Students will complete an equivalent ratio table. This activity will be conducted using an interactive whiteboard or handouts.

Example: A recipe calls for 2 cups of flour for every 3 cups of milk. Complete the equivalent ratio table:

Solution:

Explanation: To fill in the missing values, we use the relationship between flour and milk. For every 2 cups of flour, we need 3 cups of milk. So, we can multiply both the flour and milk amounts by the same factor to find equivalent ratios.

For the second column: 2 × 2 = 4 cups of flour, 3 × 2 = 6 cups of milk
For the third column: 2 × 3 = 6 cups of flour, 3 × 3 = 9 cups of milk
For the fourth column: 2 × 4 = 8 cups of flour, 3 × 4 = 12 cups of milk

Resource: https://www.media4math.com/library/card/equivalent-ratio-tables

Teach (25 minutes)

Definitions (5 minutes)

Equation: A mathematical statement that shows two expressions are equal
Coordinate plane: A two-dimensional plane formed by the intersection of a vertical line called y-axis and a horizontal line called x-axis
y-intercept: The point where a line crosses the y-axis
Slope: The steepness of a line, calculated as the change in y divided by the change in x
Unit rate: A rate where the denominator is 1
Proportional relationship: A relationship between two quantities where one quantity is a constant multiple of the other

Instruction (20 minutes)

This slide show provides an overview of proportions:

https://www.media4math.com/library/slideshow/overview-proportions

 This slide show provides multiple examples of solving proportions algebraically. Review several of these examples before moving on to the more detailed examples below:

https://www.media4math.com/library/slideshow/math-examples-solving-proportions-algebraically

Example 1: Distance and Time

Problem: A car travels at a constant speed of 60 miles per hour. Express the relationship between distance traveled (y) and time (x) as an equation.

Solution:
• The unit rate is 60 miles per hour
• Let y represent the distance traveled and x represent the time
• Equation: y = 60x

Example 2: Circle Geometry

Problem: Provide a data table and derive the equation showing that the slope is π. This could also be a hands-on activity in which students are measuring the diameters and circumferences for different circular objects. (Using a string, wrap it around the circular shape and then measure the length of the string to find the circumference.)

Solution:

• The ratio C/d is constant and approximately equal to 3.14 (π)
• This suggests a proportional relationship: C = πd
• The equation is y = πx, where y is the circumference and x is the diameter
• The slope of this line is π, which is the constant of proportionality

Example 3: Hourly Wages

Problem: Start with a data table, derive the equation, and solve a proportion.

Solution:

• Calculate the unit rate: 120 / 8 = $15 per hour
• The equation is y = 15x, where y is wages earned and x is hours worked

Solving a proportion: If someone works for 10 hours, how much will they earn?
• Use the equation: y = 15(10) = $150

Review (10 minutes)

Students will practice solving real-world problems using ratio tables and proportions.

Example 1

A store sells 5 notebooks for \$7. How many notebooks can be bought for \$42?

Solution using ratio table:

We can see that 30 notebooks can be bought for \$42.

Example 2

A car travels 210 miles in 3 hours. At this rate, how long will it take to travel 350 miles?

Solution using proportion:
• Set up the proportion: 210/3 = 350/x, where x is the time in hours
• Cross multiply: 210x = 3 * 350
• Solve for x: 210x = 1050
x = 1050/210 = 5
• Therefore, it will take 5 hours to travel 350 miles at this rate.

Assess (5 minutes)

Use this 10-question quiz to assess student understanding.

Quiz

1. Write an equation to represent a proportional relationship where y is 3 times x.
   
    
2. Graph the proportional relationship y = 2.5x.
   
   
    
3. What does the point (0,0) represent in a proportional relationship?
   
    
4. In the equation y = kx, what does k represent?
   
    
5. If a graph of a proportional relationship passes through the point (4,10), what is the unit rate?
   
    
6. A car travels 240 miles in 4 hours at a constant speed. Write an equation to represent this relationship.
   
    
7. In a proportional relationship, what does the point (1,r) represent?
   
    
8. Graph the equation y = 0.5x.
   
   
    
9. A recipe calls for 2 cups of flour for every 3 cups of milk. Write an equation to represent the relationship between flour (y) and milk (x).
   
    
10. If 4 oranges cost $2, how much would 10 oranges cost? Set up and solve a proportion.

Answer Key

1. y = 3x
2. ]
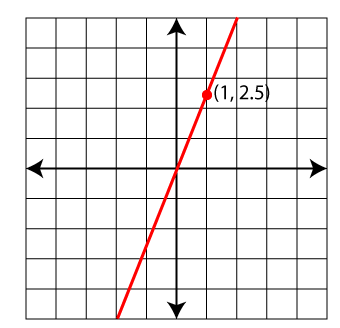3. The starting point or initial value of the relationship
4. The constant of proportionality or unit rate
5. 2.5 (10 ÷ 4 = 2.5)
6. y = 60x, where y is distance and x is time
7. The unit rate of the proportional relationship
8. 
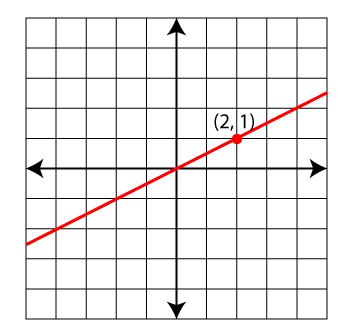
9. y = (2/3)x
10. 4/2 = 10/x, 4x = 20, x = 5. 10 oranges would cost $5.

Purchase the lesson plan bundle. Click here.