Mathematical Models

Overview
Expect to see a fairly large number of questions on the SAT that deal with mathematical models. Basically, a mathematical model is an equation, formula, or expression that can be used to solve a real-world phenomena or problem. The types of questions you’ll encounter will have you to interpret a mathematical model or develop one based on information provided.
In this section, we will review the following aspects of this topic:
- Linear Models
- Non-Linear Models
Let’s look at each of these in more detail:
Linear Models
Linear models include a linear variable. We’ll start by looking at models that are basically linear expressions
Linear Expressions
Review the topic of Linear Expressions. Here the goal is to have you build a mathematical model based on a verbal description. Here is an example.
One restaurant sold p pizzas every hour over a six-hour period. Another restaurant sold s sandwiches per hour over a seven-hour period. Write the expression that represents the total number of pizzas and sandwiches sold.
Both the variables p and s are rates. To find the total number of pizzas and sandwiches sold, multiply each rate by the number of hours:
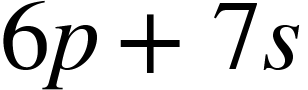
|
SAT Skill: Modeling Expressions
Example 1
A factory produces t toys per day. These toys are packed in n units per box. Write the expression that can be used to find the number of boxes needed per day.
There are two rates at work, the number of toys produced per day (t) and the number of toys per box (n). Dividing t by n results in the number of boxes needed per day.
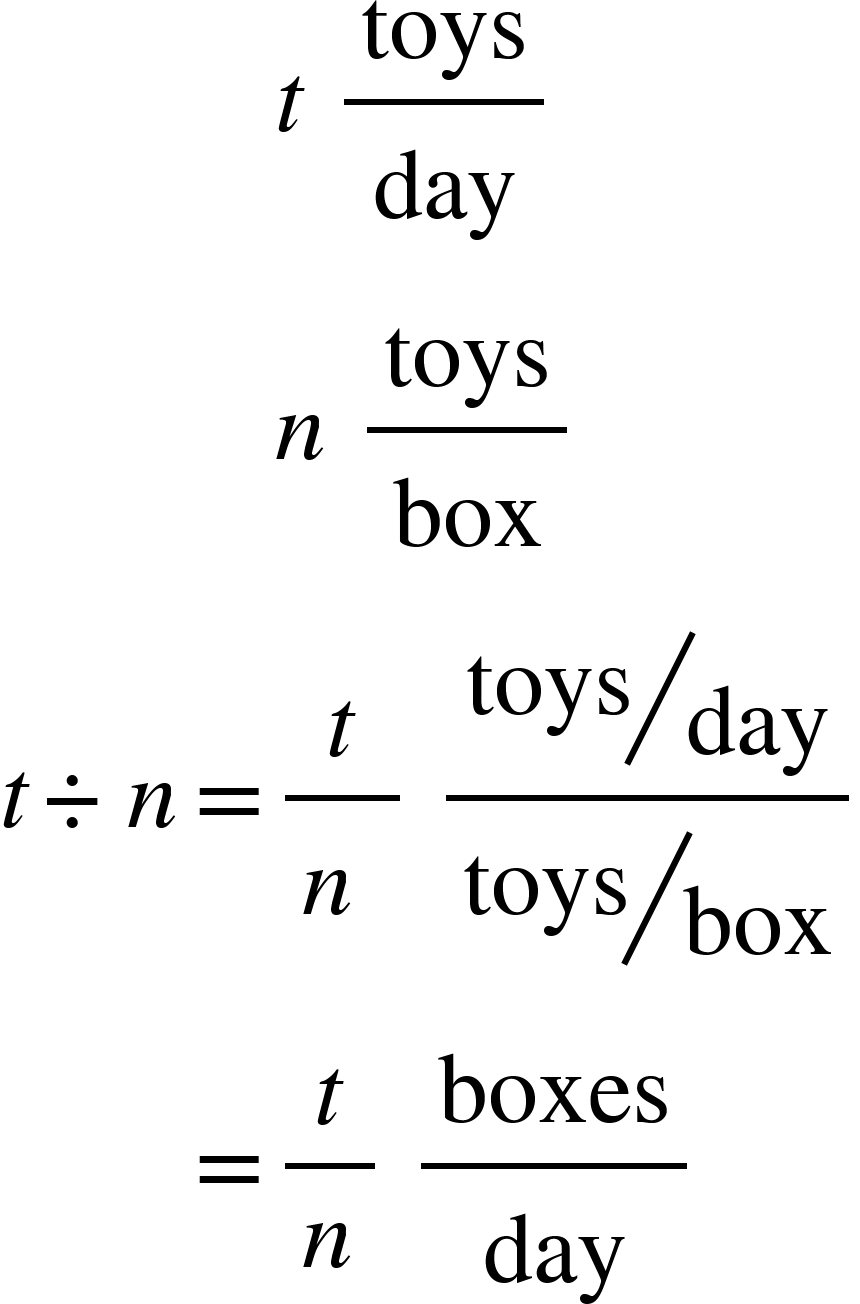
|
Linear Equations
Look for questions that ask you to analyze or build a mathematical model using a linear equation. Let’s look at an example.
A restaurant sold p pizzas in a day, and each pizza cost $10. It also sold d drinks and each drink was $2.
On a given day 175 pizzas and sodas were sold and generated $750 in revenue. How many pizzas were sold?
Here is the mathematical model for finding the dollar amount of pizzas and sodas sold:
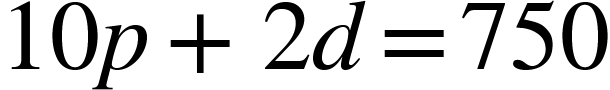
Here is the model for finding the total number of pizzas and drinks sold:

This is a system of equations, which can be solved by the Substitution Method:

So, 50 pizzas were sold.
|
SAT Skill: Modeling Linear Equations
Example 1
A technician uses this equation to estimate the number of computers that need to be repaired.

The variable C represents the estimate of the number of computers left to fix in a given month. The variable d represents the number of days elapsed in the month and ranges from 1 to 30. What does the value 120 represent?
The equation shown is a linear function.

At C(0), the function output is 120.
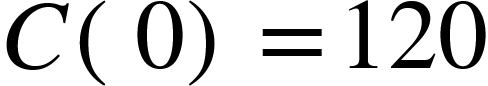
This means that before any work is started there are 120 computers left to repair. This means that the value 120 represents the expected number of computers to repair in a month.
Example 2
A company launched a new product and uses this equation to estimate the revenue from sales of the product.

In the equation the revenue R is made up of units (u) of the product sold at $25 per unit. The $10,000 are the research and development costs. What happens when R = 0?
When revenue is zero, the number of units sold, times the price of each unit, is equal to the R&D costs. This is what’s known as the break-even point.

The break-even point occurs after selling 400 units.
Example 3
These equations are used to find the price per pound for beef and pork.

The variable b represents the price of beef and the variable c represents the price of pork. The variable x represents the the number of weeks after July 1, when the availability of beef and pork was at its peak. After how many weeks would the price of beef and pork be equal?
If the price of beef and pork are equal, then you have this equation:

Replace the variables with their corresponding expressions with x and then solve for x:
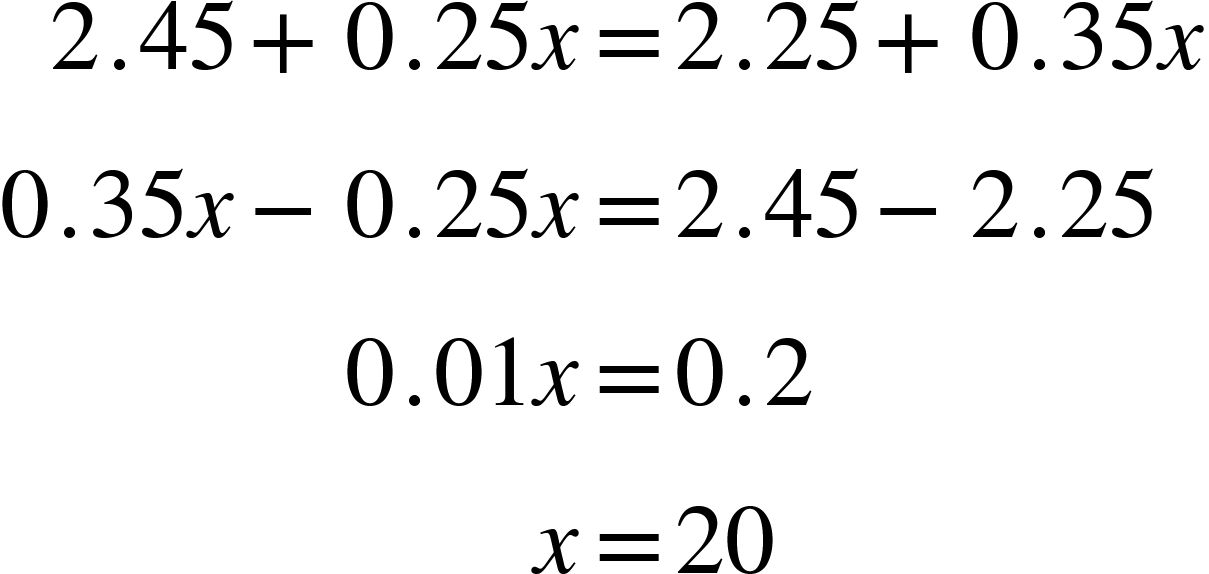
|
Non-Linear Models
Non-linear models can include quadratic equations or polynomial equations. You should review the Quadratic Functions and Equations section. Expect to see questions that involve either analyzing or developing a non-linear model of real-world situation. Let’s look at an example.
A ball is kicked from the ground level. The height (h) of the ball above the ground is modeled by this equation:

In the equation the variable t is the elapsed time (in seconds). The ball is kicked with a vertical speed of 20 meters per second. How long is the ball in the before it lands on the ground?
The equation shown is an example of a quadratic model. To find when the ball hits the ground is the same as solving this quadratic equation:
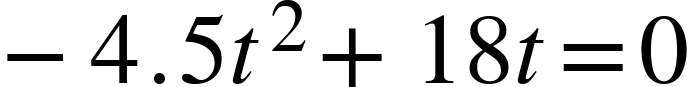
This quadratic is easily factored to find the two solutions:
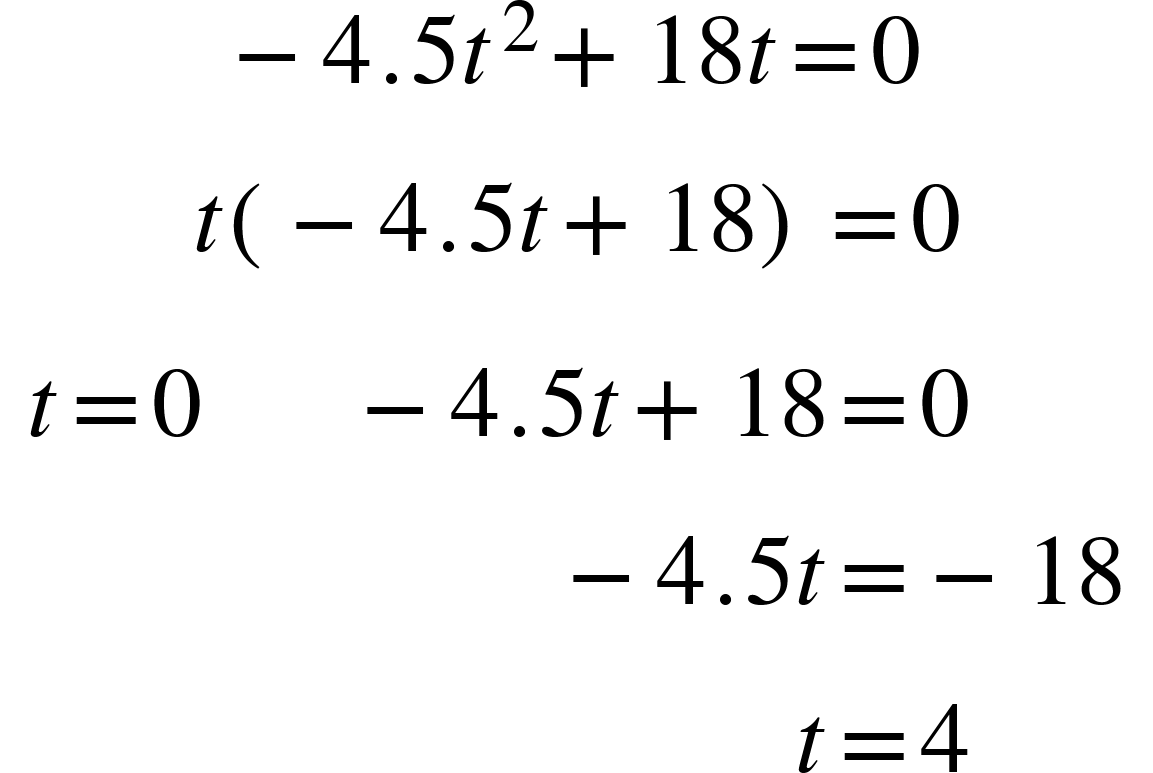
The ball will hit the ground after 4 seconds.
|
SAT Skill: Non-Linear Models
Example 1
The equation below shows the height (h), in feet, of a ball t seconds after it is thrown straight up in the air from a height of k feet at a vertical speed of v. Write the equation that is the relative change in height.
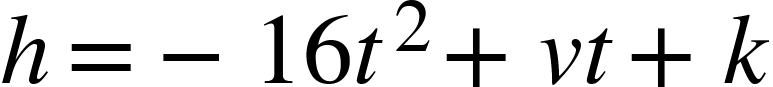
The change in height is the difference between h(t) and the initial height k.

Example 2
A rectangle of length L and width W will have 64 feet of fencing around it. Find the measures of length and width that will also have maximum area.

For this question, you’ll need to develop the math model. Let’s start with a model for the perimeter, based on the information provided:
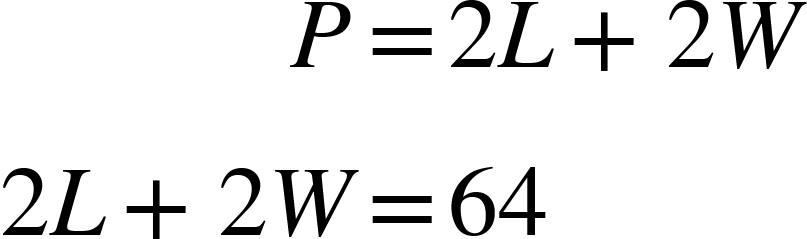
From the perimeter equation we can write L in terms of W, as shown:

We can now develop a mathematical model for the Area that will only have one variable:

This is a quadratic model that has this graph:
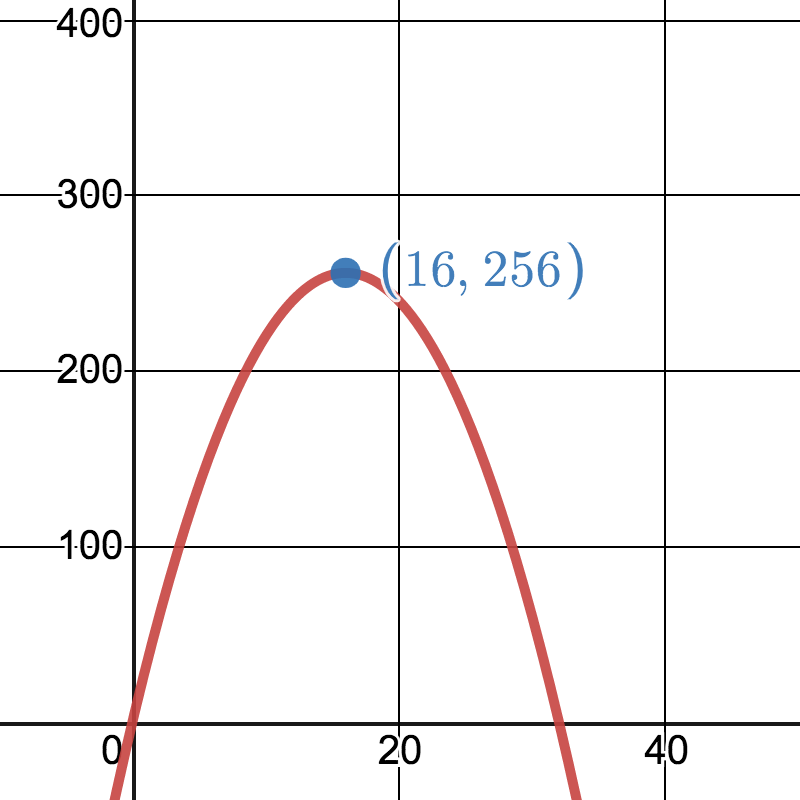
The maximum value for this parabola is at the vertex, where W = 16. We can use this value for W to find the value for L:
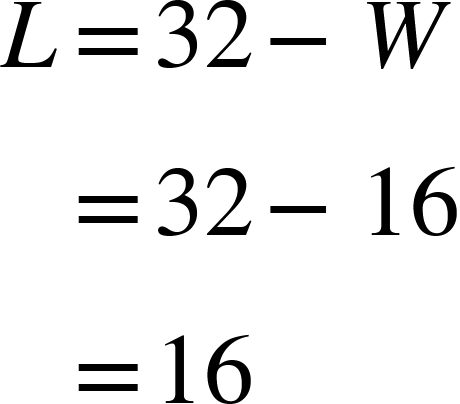
This means that the rectangle with the maximum area for a given perimeter of 64 is a square of side length 16
|
About Media4Math
All of the resources in this overview can be found on Media4Math. Subscribers can download these resources, or create their own slide shows using Slide Show Creator.