
Illustrative Math Alignment: Grade 7 Unit 3
Measuring Circles
Lesson 11: Stained-Glass Windows
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Math Clip Art--Venn Diagram 1 | Math Clip Art--Venn Diagram 1
This is part of a collection of math clip art images that show Venn Diagrams. |
Applications of Circles |
|
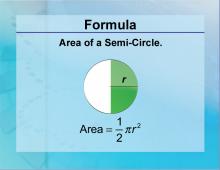
Formulas--Area of a Semi-Circle | Formulas--Area of a Semi-Circle
The formula for: Area of a Semi-Circle. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |
|
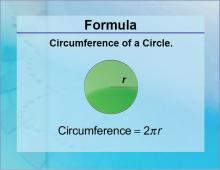
Formulas--Circumference of a Circle | Formulas--Circumference of a Circle
The formula for the Circumference of a Circle. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |
|
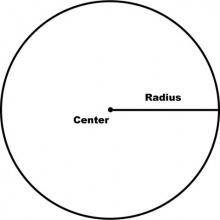
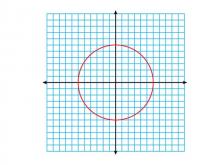
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle | Math Clip Art--Circle Illustrations--CircleTopicGeometry Concepts DescriptionThis clip art illustrates a basic circle, which is a fundamental shape in geometry. A circle is defined as the set of all points in a plane that are equidistant from a central point. This image serves as a visual representation of this concept, showcasing the perfect symmetry and continuous curvature that characterize circles. |
Definition of a Circle |
|
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered at Origin of Coordinate Grid | Math Clip Art--Circle Illustrations--Circle Centered at Origin of Coordinate GridTopicGeometry Concepts DescriptionThis clip art depicts a circle centered at the origin (0,0) of a coordinate grid. It illustrates the relationship between circles and the Cartesian coordinate system, a fundamental concept in analytic geometry. The image shows how a circle's position can be defined in relation to the x and y axes. |
Definition of a Circle |
|
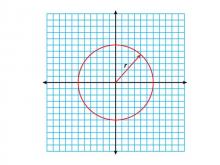
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered at Origin of Coordinate Grid--with Radius Labeled | Math Clip Art--Circle Illustrations--Circle Centered at Origin of Coordinate Grid--with Radius LabeledTopicGeometry Concepts DescriptionThis clip art shows a circle centered at the origin of a coordinate grid with its radius clearly labeled. This illustration is crucial for understanding the relationship between a circle's radius and its equation in the coordinate plane. The labeled radius helps visualize how the distance from the center to any point on the circle remains constant, which is the defining property of a circle. |
Definition of a Circle |
|
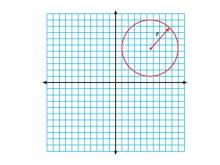
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q1 | Math Clip Art--Circle Illustrations--Circle Centered in Q1TopicGeometry Concepts DescriptionThis clip art illustrates a circle centered in the first quadrant (Q1) of the coordinate plane. This representation is crucial for understanding how the position of a circle's center affects its equation and properties. In Q1, both x and y coordinates of the center are positive, which influences the circle's equation and its intersection with the axes. |
Definition of a Circle |
|
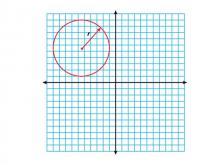
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q2 | Math Clip Art--Circle Illustrations--Circle Centered in Q2TopicGeometry Concepts DescriptionThis clip art shows a circle centered in the second quadrant (Q2) of the coordinate plane. In Q2, the x-coordinate of the center is negative while the y-coordinate is positive. This positioning is crucial for understanding how the location of a circle's center affects its equation and its relationship with the coordinate axes. |
Definition of a Circle |
|
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q3 | Math Clip Art--Circle Illustrations--Circle Centered in Q3TopicGeometry Concepts DescriptionThis clip art depicts a circle centered in the third quadrant (Q3) of the coordinate plane. In Q3, both the x and y coordinates of the center are negative. This positioning is essential for understanding how the location of a circle's center influences its equation and its interactions with the coordinate axes. |
Definition of a Circle |
|
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q4 | TopicGeometry Concepts DescriptionThis clip art illustrates a circle centered in the fourth quadrant (Q4) of the coordinate plane. In Q4, the x-coordinate of the center is positive while the y-coordinate is negative. This positioning is crucial for understanding how the location of a circle's center affects its equation and its relationship with the coordinate axes. |
Definition of a Circle |
|
Math Clip Art--Statistics and Probability--Circle Graph | Math Clip Art--Statistics and Probability--Circle Graph
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle | Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle
This is part of a collection of math clip art images about selected topics in Geometry. Also look at our Geometry Basics math clip art collection. |
Definition of a Circle and Applications of Coordinate Geometry |

|
Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle | Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle
This is part of a collection of math clip art images about selected topics in Geometry. Also look at our Geometry Basics math clip art collection. |
Definition of a Circle and Applications of Coordinate Geometry |
|
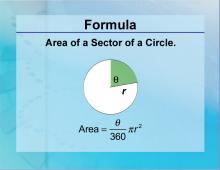
Formulas--Area of a Sector of a Circle | Formulas--Area of a Sector of a Circle
The formula for: Area of a Sector of a Circle. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |
|
Math Clip Art--Venn Diagram 2 | Math Clip Art--Venn Diagram 2
This is part of a collection of math clip art images that show Venn Diagrams. |
Applications of Circles |

|
Video Transcript: Geometry Applications: Circles | Video Transcript: Geometry Applications: Circles
This is the transcript for the video of same title. Video contents: In this program we explore the properties of circles. We do this in the context of two real-world applications. In the first, we look at the design of the Roman Coliseum and explore how circular shapes could have been used to design this elliptical structure. In the second application we look at the Roman Pantheon, specifically its spherical dome, to see how the properties of chords and secants help clarify its unique design. |
Applications of Circles |

|
Video Transcript: Geometry Applications: Circles, Segment 1: The Basics of Circles | Video Transcript: Geometry Applications: Circles, Segment 1: The Basics of Circles
This is the transcript for the video of same title. Video contents: We visit Chaco Canyon in New Mexico to explore the circular kivas and in the process discover how circular buildings have been used to study the heavens. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Circles |

|
Video Transcript: Geometry Applications: Circles, Segment 2: Circles and Arcs | Video Transcript: Geometry Applications: Circles, Segment 2: Circles and Arcs
This is the transcript for the video of same title. Video contents: The Roman Coliseum is a large elliptical structure. Yet, the Romans likely used circular arcs to build it. This segment explores the properties of circles and shows how arcs can be used to create elliptical shapes. |
Applications of Circles |

|
Video Transcript: Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles | Video Transcript: Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles
This is the transcript for the video of same title. Video contents: The Roman Pantheon is a domed structure that shows a keen awareness of the position of the sun throughout the year. The source of light from the top of the dome allows for the exploration of chords, inscribed angles, central angles, and intercepted arcs. |
Applications of Circles |

|
Geometry Applications Teachers Guide: Circles | Geometry Applications Teachers Guide: Circles
This is the Teacher's Guide that accompanies Geometry Applications: Circles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |

|
Worksheet: Crossword Puzzle--Circles | Worksheet: Crossword Puzzle--Circles
This is part of a collection of math worksheets that are crossword puzzles of math vocabulary. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Definition of a Circle |

|
Worksheet: TI-Nspire Mini-Tutorial: Circumscribing a circle about a triangle | Worksheet: TI-Nspire Mini-Tutorial: Circumscribing a circle about a triangle
This is part of a collection of math worksheets on the use of the TI-Nspire graphing calculator. Each worksheet supports a companion TI-Nspire Mini-Tutorial video. It provides all the keystrokes for the activity. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Geometric Constructions with Triangles |
|
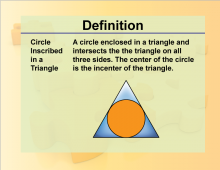
Definition--Geometry Basics--Circle Inscribed In a Triangle | Circle Inscribed In a TriangleTopicGeometry Basics DefinitionA circle that is tangent to all three sides of a triangle. DescriptionA circle inscribed in a triangle is a circle that is tangent to all three sides of the triangle. This concept is important in understanding the properties of triangles and their relationship with circles. For example, the radius of the inscribed circle can be used to calculate the area of the triangle using the formula Area = 1/2 × perimeter × radius. Understanding inscribed circles helps in solving problems related to triangle geometry and optimization. |
Definition of a Circle |
|
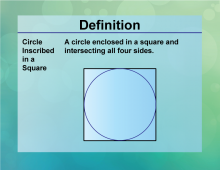
Definition--Circle Concepts--Circle Inscribed in a Square | Circle Inscribed in a SquareTopicCircles DefinitionA circle inscribed in a square touches all four sides of the square at exactly one point each. |
Definition of a Circle |
|
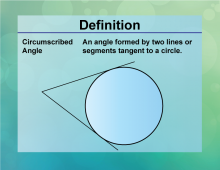
Definition--Circle Concepts--Circumscribed Angle | Circumscribed AngleTopicCircles DefinitionA circumscribed angle is an angle formed outside a circle by two intersecting tangents. |
Definition of a Circle |

|
SAT Math Lesson Plan 26: Circle Theorems and Tangents | SAT Math Lesson Plan 26: Circle Theorems and Tangents In SAT Math Lesson 26, students will explore important geometric theorems involving circles, tangents, and inscribed angles. This lesson covers:
|
Geometric Constructions with Circles |
|
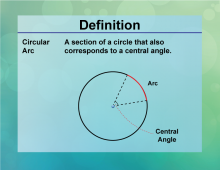
Definition--Circle Concepts--Circular Arc | Circular ArcTopicCircles DefinitionA circular arc is a portion of the circumference of a circle. DescriptionCircular arcs are segments of a circle's circumference, used extensively in design, architecture, and engineering to create curved structures and paths. The length of an arc is determined by the central angle and the circle's radius, calculated using the formula L = rθ |
Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 1 | VIDEO: Geometry Applications: Circles, 1
TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |
|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Math in the News: Issue 88--Examining the Polar Vortex | Math in the News: Issue 88--Examining the Polar Vortex
January 2014. In this issue of Math in the News we examine the Polar Vortex. We examine the physics of the cyclonic winds that make up the Polar Vortex and under what conditions the current expansion of Arctic weather affects a large part of the United States. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |

|
Promethean Flipchart: Geometry Applications: Circles 1 | The Roman Coliseum is a large elliptical structure. Yet, the Romans likely used circular arcs to build it. This segment explores the properties of circles and shows how arcs can be used to create elliptical shapes. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Circles, Segment 2: Circles and Arcs]: https://www.media4math.com/library/geometry-applications-circles-segment-2-circles-and-arcs This video includes a video transcript: https://media4math.com/library/video-transcript-geometry-applications-circles-segment-2-circles-and-arcs |
Applications of Circles |

|
Promethean Flipchart: Geometry Applications: Circles 2 | The Roman Pantheon is a domed structure that shows a keen awareness of the position of the sun throughout the year. The source of light from the top of the dome allows for the exploration of chords, inscribed angles, central angles, and intercepted arcs. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Circles, Segment 3: Chords and Inscribed Angles]: https://media4math.com/library/geometry-applications-circles-segment-3-chords-and-inscribed-angles This video includes a Video Transcript: https://www.media4math.com/library/video-transcript-geometry-applications-circles-segment-3-chords-and-inscribed-angles |
Applications of Circles |

|
Google Earth Voyager Story: Circular Structures, Part 1 | Google Earth Voyager Story: Circular Structures, Part 1TopicGeometric Models |
Applications of Circles |

|
Google Earth Voyager Story: Circular Structures, Part 2 | Google Earth Voyager Story: Circular Structures, Part 2TopicGeometric Models |
Applications of Circles and Cylinders |

|
VIDEO: Geometry Applications: Circles | VIDEO: Geometry Applications: Circles
TopicCircles |
Applications of Circles |
|
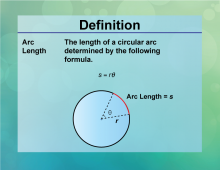
Definition--Circle Concepts--Arc Length | Arc LengthTopicCircles DefinitionAn arc length is the distance along the curved line making up the arc. DescriptionThe arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula L = rθ |
Definition of a Circle |
|
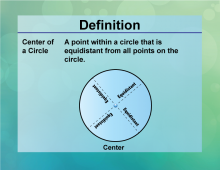
Definition--Circle Concepts--Center of a Circle | Center of a CircleTopicCircles DefinitionThe center of a circle is the point equidistant from all points on the circle. DescriptionThe center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation |
Definition of a Circle |

|
Definition--Circle Concepts--Chord | ChordTopicCircles DefinitionA chord is a line segment with both endpoints on the circle. |
Definition of a Circle |
|
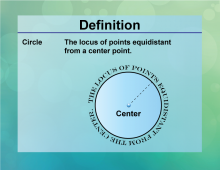
Definition--Circle Concepts--Circle | CircleTopicCircles DefinitionA circle is a set of all points in a plane equidistant from a given point, the center. DescriptionThe circle is one of the most fundamental shapes in geometry, characterized by its symmetry and uniformity. It is used extensively in various fields, including engineering, design, and astronomy, where its properties are applied to create wheels, gears, and orbits. Mathematically, a circle is defined by its center and radius, and its equation in a plane is (x − h)2 + (y − k)2 = r2 |
Definition of a Circle |

|
Definition--Charts and Graphs--Circle Graph | Definition--Charts and Graphs--Circle Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
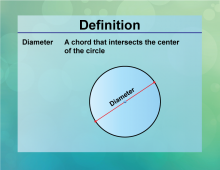
Definition--Circle Concepts--Diameter | DiameterTopicCircles DefinitionThe diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. DescriptionThe diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr |
Definition of a Circle |
|
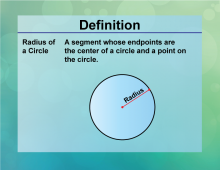
Definition--Circle Concepts--Radius of a Circle | Radius of a CircleTopicCircles DefinitionThe radius of a circle is a line segment from the center to any point on the circle. |
Definition of a Circle |
|
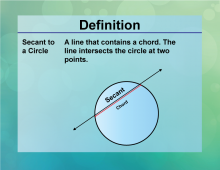
Definition--Circle Concepts--Secant to a Circle | Secant to a CircleTopicCircles DefinitionA secant is a line that intersects a circle at two points. DescriptionSecants are significant in geometry, representing lines that intersect a circle at two distinct points. These lines are used in various applications, such as in design and architecture, where precise measurements of angles and distances are essential. In mathematics, secants are explored in the context of circle theorems, providing insights into the properties of lines and circles. In education, understanding secants helps students develop geometric reasoning and problem-solving skills, which are essential for advanced studies in geometry and trigonometry. |
Definition of a Circle |

|
Definition--Circle Concepts--Sector | SectorTopicCircles DefinitionA sector is a portion of a circle enclosed by two radii and the arc between them. DescriptionSectors are fundamental in the study of circles, representing a portion of the circle's area. These shapes are used in various applications, such as in design and architecture, where precise measurements of angles and areas are essential. The area of a sector is calculated using the formula A = 1/2r2θ |
Definition of a Circle |
|
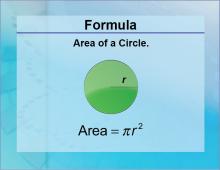
Formulas--Area of a Circle | Formulas--Area of a Circle
The formula for the Area of a Circle. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |