
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 18: Comparing Populations Using Samples
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Measures of Central Tendency: Quizlet Flash Cards | This is a collection of Quizlet Flash Cards on various topics in Measures of Central Tendency.
|
Data Analysis |

|
Measures of Central Tendency: Worksheets | Here is a collection of worksheets on various topics in Measures of Central Tendency.
|
Data Analysis |

|
Video Tutorials: Measures of Central Tendency | This is a collection of video tutorials, transcripts, and closed captioned videos on measures of central tendency.
|
Data Analysis and Data Gathering |

|
Math Examples Collection: Range | OverviewThis collection of math examples focuses on Measures of Central Tendency, specifically the concept of Range. It comprises 26 downloadable JPG images that educators can easily incorporate into their lesson plans. |
Data Analysis |

|
Math Worksheet Collection: Data Analysis: Mean, Median, and Mode | Math Worksheet Collection: Data Analysis: Mean, Median, and Mode OverviewThis collection aggregates all the math worksheets around the topic of Data Analysis: Mean, Median, and Mode. There are a total of 60 worksheets. Each worksheet includes an answer key. This collection of resources is made up of downloadable PDF files that you can easily incorporate into your instruction.
|
Data Analysis |

|
Math Clip Art Collection: Statistics |
OverviewThis collection aggregates all the math clip art around the topic of Statistics. There are a total of 55 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.To download the full set of these resources, click on this link.
|
Data Analysis, Probability, Data Gathering and Counting |

|
Math Video Collection: Video Tutorials Series: Measures of Central Tendency |
OverviewThis collection aggregates all the math videos and resources in this series: Video Tutorials Series: Measures of Central Tendency. There are a total of 24 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
Data Analysis and Data Gathering |

|
Quizlet Flash Card Collection: Measures of Central Tendency |
OverviewThis is a collection of Quizlet Flash Cards on the topic of Measures of Central Tendency. There are a total of 20 Quizlet Flash Card sets.
|
Data Analysis |

|
Quizlet Flash Card Collection: Find The Middle Term |
OverviewThis is a collection of Quizlet Flash Cards on the topic of Finding the Middle Term. There are a total of 5 Quizlet Flash Card sets.
|
Compare and Order Numbers |

|
Math in the News Collection: Applications of Data Analysis |
OverviewThis is a collection of Math in the News stories that focus on the topic of Data Analysis.
|
Data Analysis, Data Gathering, Probability, Percents and Ratios and Rates |

|
Measures of Central Tendency: Math Examples IV | Here is a collection of detailed math examples on the topic of the Range.
|
Data Analysis |

|
Closed Captioned Video: Measures of Central Tendency: Finding the Mean of a Data Set I | Closed Captioned Video: Measures of Central Tendency: Finding the Mean of a Data Set I
In this video tutorial students learn how to calculate the mean when all of the data items are positive numbers. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Finding the Mean of a Data Set II | Closed Captioned Video: Measures of Central Tendency: Finding the Mean of a Data Set II
In this video tutorial students learn how to calculate the mean when some of the data items are negative numbers. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Finding the Median of a Data Set | Closed Captioned Video: Measures of Central Tendency: Finding the Median of a Data Set
In this video tutorial students learn how to find the median of a data set. The mean is also calculated so that students can learn similarities and differences between these two measures of central tendency. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Finding the Mode of a Data Set | Closed Captioned Video: Measures of Central Tendency: Finding the Mode of a Data Set
In this video tutorial students learn how to calculate the mode of a data set, as well as how the mode differs from the mean and median.Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Mean of a Probability Distribution | Closed Captioned Video: Measures of Central Tendency: Mean of a Probability Distribution
In this video tutorial students learn about the mean of a probability distribution. Includes a brief discussion of expected value, plus a brief tie-in to weighted means. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Sample Mean | Closed Captioned Video: Measures of Central Tendency: Sample Mean
In this video tutorial students learn about sample mean from a random sampling of data. All examples involve normally distributed data with a known population mean and standard deviation. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: The Mean and Normally Distributed Data | Closed Captioned Video: Measures of Central Tendency: The Mean and Normally Distributed Data
In this video tutorial students learn about normally distributed data and how to identify the population mean from the normal distribution. Standard deviation is briefly introduced. Includes three real-world examples. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Measures of Central Tendency: Weighted Mean | Closed Captioned Video: Measures of Central Tendency: Weighted Mean
In this video tutorial students extend their understanding of mean by looking at examples of weighted means (sometimes referred to as weighted averages). Includes three real-world examples. |
Data Analysis and Data Gathering |
|
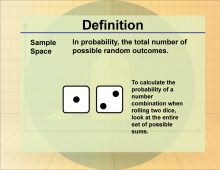
Definition--Statistics and Probability Concepts--Sample Space | Sample SpaceTopicStatistics and Probability DefinitionA sample space is the set of all possible outcomes in a probability experiment. DescriptionThe sample space is a foundational concept in probability, providing the framework within which probabilities are assigned to events. It is used in various fields, such as finance, to model different investment outcomes, or in engineering to predict system failures. Understanding the sample space is crucial for students to accurately calculate probabilities and analyze different scenarios. It helps them develop a comprehensive understanding of how different events relate to each other within a probability model. |
Probability |
|
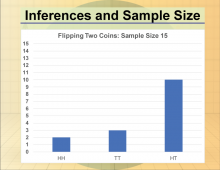
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--10 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--10
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
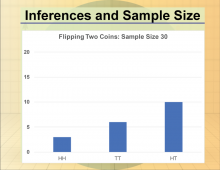
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--11 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--11
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
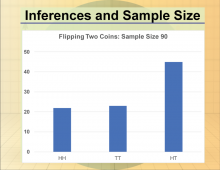
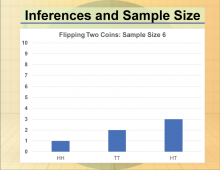
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--12 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--12
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
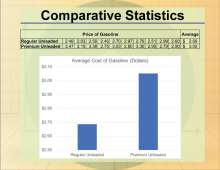
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--9 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--9
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
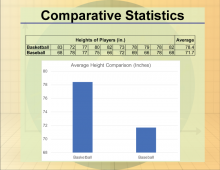
Math Clip Art--Statistics--Comparative Statistic--02 | Math Clip Art--Statistics--Comparative Statistic--02
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
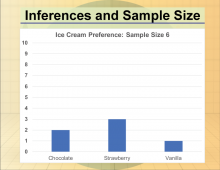
Math Clip Art--Statistics--Comparative Statistics--01 | Math Clip Art--Statistics--Comparative Statistics--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
Math Clip Art--Statistics--Inferences and Sample Size--01 | Math Clip Art--Statistics--Inferences and Sample Size--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
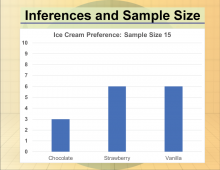
|
Math Clip Art--Statistics--Inferences and Sample Size--02 | Math Clip Art--Statistics--Inferences and Sample Size--02
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
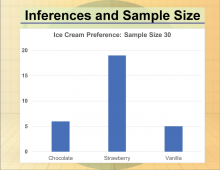
|
Math Clip Art--Statistics--Inferences and Sample Size--03 | Math Clip Art--Statistics--Inferences and Sample Size--03
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
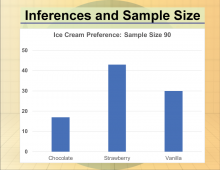
|
Math Clip Art--Statistics--Inferences and Sample Size--04 | Math Clip Art--Statistics--Inferences and Sample Size--04
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
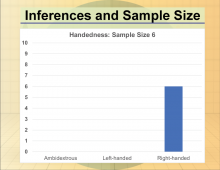
|
Math Clip Art--Statistics--Inferences and Sample Size--05 | Math Clip Art--Statistics--Inferences and Sample Size--05
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
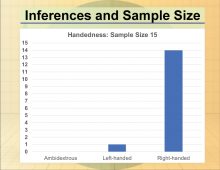
|
Math Clip Art--Statistics--Inferences and Sample Size--06 | Math Clip Art--Statistics--Inferences and Sample Size--06
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
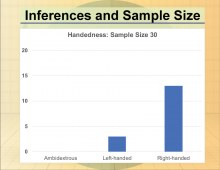
|
Math Clip Art--Statistics--Inferences and Sample Size--07 | Math Clip Art--Statistics--Inferences and Sample Size--07
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
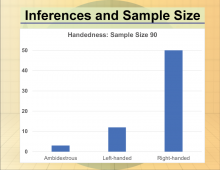
|
Math Clip Art--Statistics--Inferences and Sample Size--08 | Math Clip Art--Statistics--Inferences and Sample Size--08
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |

|
Math Example--Measures of Central Tendency--Range: Example 1 | Math Example--Measures of Central Tendency--Range: Example 1TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 10 | Math Example--Measures of Central Tendency--Range: Example 10TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 11 | Math Example--Measures of Central Tendency--Range: Example 11TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 12 | Math Example--Measures of Central Tendency--Range: Example 12TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 13 | Math Example--Measures of Central Tendency--Range: Example 13TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 14 | Math Example--Measures of Central Tendency--Range: Example 14TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 15 | Math Example--Measures of Central Tendency--Range: Example 15TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |
|
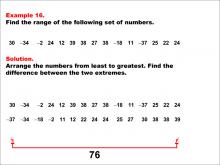
Math Example--Measures of Central Tendency--Range: Example 16 | Math Example--Measures of Central Tendency--Range: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |
|
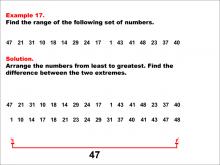
Math Example--Measures of Central Tendency--Range: Example 17 | Math Example--Measures of Central Tendency--Range: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 18 | Math Example--Measures of Central Tendency--Range: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 19 | Math Example--Measures of Central Tendency--Range: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 2 | Math Example--Measures of Central Tendency--Range: Example 2TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 20 | Math Example--Measures of Central Tendency--Range: Example 20TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |
|
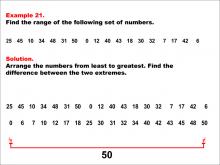
Math Example--Measures of Central Tendency--Range: Example 21 | Math Example--Measures of Central Tendency--Range: Example 21TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
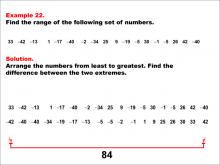
Math Example--Measures of Central Tendency--Range: Example 22 | Math Example--Measures of Central Tendency--Range: Example 22TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 23 | Math Example--Measures of Central Tendency--Range: Example 23TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |