
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 15: The Volume of a Cone
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Holiday Themed Resource Collection: Math in the News |
This is a collection of Holiday-Themed issues of Math in the News.
|
Data Analysis, Applications of Exponential and Logarithmic Functions, Surface Area and Volume |

|
Lesson Plan Collection: Cross-Sections of 3D Figures | Cross-Sections of 3D Figures | 3-Lesson Unit This collection of geometry lesson plans explores how slicing three-dimensional figures produces different cross-sections. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Math in the News Collection: Applications of Surface Area and Volume |
OverviewThis is a collection of issues of Math in the News that deal with applications of Surface Area and Volume.
|
Surface Area and Volume |

|
Math in the News Collection: Applications of 3D Geometry |
OverviewThis is a collection of issues of Math in the News that deal with applications of 3D geometry.
|
3-Dimensional Figures and Applications of 3D Geometry |

|
Math in the News Collection: Business Math |
OverviewThis is a collection of issues of Math in the News that deal with business applications.
|
Applications of Exponential and Logarithmic Functions, Data Analysis and Volume |

|
Math in the News Collection: Applications of Data Analysis |
OverviewThis is a collection of Math in the News stories that focus on the topic of Data Analysis.
|
Data Analysis, Data Gathering, Probability, Percents and Ratios and Rates |

|
Math Video Collection: 3D Geometry Animations |
OverviewThis collection aggregates all the math videos and resources in this series: 3D Geometry Animations. There are a total of 10 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
3-Dimensional Figures, Cubes, Cones, Triangular Prisms, Pyramids, Cylinders and Rectangular Prisms |

|
Math Video Collection: Geometry Applications Video Series: 3D Geometry | OverviewThis collection aggregates all the math videos and resources in this series: Geometry Applications Video Series: 3D Geometry. There are a total of 18 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
3-Dimensional Figures, Applications of 3D Geometry, Pyramids, Cylinders, Rectangular Prisms and Triangular Prisms |
|
Math Examples Collection: Volume | OverviewThis collection of math examples on the topic of Volume provides students with an in-depth exploration of volume concepts through a variety of visual models. Covering a range of skills and increasing in complexity, this collection helps students master foundational and advanced topics in volume. From calculating the volume of basic geometric shapes to applying volume formulas to complex objects, these examples build confidence and enhance comprehension by breaking down challenging concepts visually. |
Volume |

|
VIDEO: 3D Geometry Animation: Antiprism | VIDEO: 3D Geometry Animation: Antiprism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Triangular Prisms |

|
VIDEO: 3D Geometry Animation: Cone | VIDEO: 3D Geometry Animation: Cone
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cones |

|
VIDEO: 3D Geometry Animation: Cube | VIDEO: 3D Geometry Animation: Cube
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cubes |

|
VIDEO: 3D Geometry Animation: Cylinder | 3D Geometry Animation: Cylinder
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cylinders |

|
VIDEO: 3D Geometry Animation: Octahedron | VIDEO: 3D Geometry Animation: Octahedron
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
VIDEO: 3D Geometry Animation: Pyramid | VIDEO: 3D Geometry Animation: Pyramid
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Pyramids |

|
VIDEO: 3D Geometry Animation: Rectangular Prism | VIDEO: 3D Geometry Animation: Rectangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Rectangular Prisms |

|
VIDEO: 3D Geometry Animation: Tetrahedron | VIDEO: 3D Geometry Animation: Tetrahedron
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
VIDEO: 3D Geometry Animation: Triangular Prism | VIDEO: 3D Geometry Animation: Triangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Horizontal Cross-Section of a Rectangular Prism | Animated Math Clip Art: Horizontal Cross-Section of a Rectangular Prism This animated math clip art illustrates how a horizontal plane intersects a rectangular prism, forming a two-dimensional cross-section. As the plane moves through the prism, students can observe that the resulting cross-section is always a rectangle, reinforcing key geometric concepts related to slicing three-dimensional shapes. Ideal for classroom instruction, this GIF animation helps students develop spatial reasoning by demonstrating how horizontal slices interact with the structure of a rectangular prism. This visual aid is particularly useful for teaching cross-sections in geometry, emphasizing how different slicing directions produce distinct 2D shapes. |
Rectangular Prisms |

|
Animated Math Clip Art--3D Geometry--Rotating a Triangle to Form a Cone | Rotating a Triangle to Form a ConeTopic3D Geometry DescriptionThis animation shows how rotating a triangle around one of its sides creates a cone. It's a powerful visualization of how 2D shapes can generate 3D objects through rotation. Animated math clip art like this is crucial for teaching as it helps students visualize the formation of cones. Teachers can use this to introduce concepts of volume and surface area of cones, as well as topics in calculus related to solids of revolution. |
Cones |

|
Animated Math Clip Art--3D Geometry--Vertical Cross-Section of a Rectangular Prism | Animated Math Clip Art: Vertical Cross-Section of a Rectangular Prism This animated math clip art visually demonstrates how a vertical plane intersects a rectangular prism, producing a two-dimensional cross-section. As the plane moves through the 3D shape, students can observe how the resulting cross-section remains a rectangle, reinforcing key geometric concepts related to slicing three-dimensional figures. Perfect for classroom instruction, this GIF animation helps students develop spatial reasoning by illustrating how a vertical slice interacts with the faces of a rectangular prism. This resource is particularly useful for teaching cross-sections in geometry and preparing students to understand more complex 3D slicing concepts. |
Rectangular Prisms |

|
Closed Captioned Video: Geometry Applications: 3D Geometry | Closed Captioned Video: Geometry Applications: 3D GeometryTopic3D Geometry |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 1 | Closed Captioned Video: Geometry Applications: 3D Geometry, 1Topic3D Geometry DescriptionDescription: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 2 | Closed Captioned Video: Geometry Applications: 3D Geometry, 2Topic3D Geometry DescriptionDescription: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences. |
3-Dimensional Figures, Pyramids and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 3 | Closed Captioned Video: Geometry Applications: 3D Geometry, 3Topic3D Geometry DescriptionDescription: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency. |
3-Dimensional Figures, Cylinders and Applications of 3D Geometry |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 | INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 1 | Lesson Plan: Cross-Sections of 3D Figures In this engaging math lesson, students explore cross-sections of cubes, cylinders, and cones through interactive activities, real-world examples, and animated visuals. They will learn how slicing three-dimensional shapes in different ways produces a variety of two-dimensional figures, helping to develop spatial reasoning and geometric understanding. The lesson begins with a conceptual introduction to cross-sections, followed by hands-on practice with everyday objects such as gift boxes, paper towel rolls, and ice cream cones. Students will investigate how horizontal, vertical, and diagonal slices impact the resulting shapes. Animated GIFs illustrate these concepts, reinforcing learning through dynamic visual representations. |
3-Dimensional Figures |
|
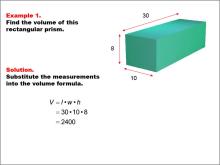
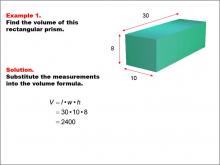
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
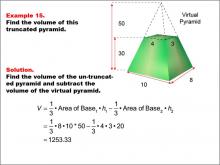
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
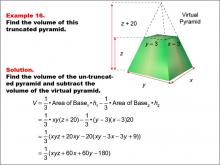
|
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
|
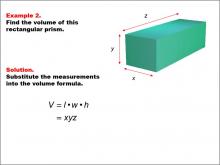
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 4 | Math Example--Volume Concepts--Calculating Volume: Example 4TopicVolume DescriptionA hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2). |
Volume |
|
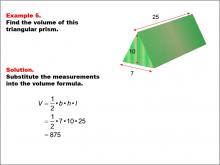
Math Example--Volume Concepts--Calculating Volume: Example 5 | Math Example--Volume Concepts--Calculating Volume: Example 5TopicVolume DescriptionThe image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875. |
Volume |
|
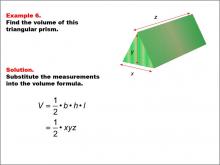
Math Example--Volume Concepts--Calculating Volume: Example 6 | Math Example--Volume Concepts--Calculating Volume: Example 6TopicVolume DescriptionThe image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 7 | Math Example--Volume Concepts--Calculating Volume: Example 7TopicVolume DescriptionThe image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525.. |
Volume |