
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 2: Finding Area by Decomposing and Rearranging
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Clip Art--Geometry Concepts--Composite Figures--Composite Figure 7 |
Math Clip Art--Composite Figures--Composite Figure 7TopicGeometry Concepts DescriptionThis image depicts a composite figure consisting of two adjacent regular hexagons. This configuration is often found in nature, such as in honeycomb structures, and is used in various design and engineering applications. To calculate the total area of this figure, we would add the areas of the two hexagons (given by the formula A = (3√3 * s²) / 2, where s is the side length). The perimeter would involve summing the lengths of all outer sides, excluding the shared edge between the hexagons. |
Applications of Polygons |

|
Math Clip Art--Geometry Concepts--Composite Figures--Composite Figure 8 |
Math Clip Art--Composite Figures--Composite Figure 8TopicGeometry Concepts DescriptionThis image illustrates a composite figure composed of two regular hexagons connected by a square. This unique configuration combines the properties of hexagons and squares in an interesting geometric arrangement. To calculate the total area of this figure, we would add the areas of the two hexagons (A = (3√3 * s²) / 2 for each, where s is the side length) and the area of the connecting square (s²). The perimeter would involve summing the lengths of all outer sides of the figure. |
Applications of Polygons |

|
Math Clip Art--Geometry Concepts--Composite Figures--Composite Figure 8 |
Math Clip Art--Composite Figures--Composite Figure 8TopicGeometry Concepts DescriptionThis image illustrates a composite figure composed of two regular hexagons connected by a square. This unique configuration combines the properties of hexagons and squares in an interesting geometric arrangement. To calculate the total area of this figure, we would add the areas of the two hexagons (A = (3√3 * s²) / 2 for each, where s is the side length) and the area of the connecting square (s²). The perimeter would involve summing the lengths of all outer sides of the figure. |
Applications of Polygons |

|
Math Clip Art--Geometry Concepts--Composite Figures--Composite Figure 9 |
Math Clip Art--Composite Figures--Composite Figure 9TopicGeometry Concepts DescriptionThis image shows a composite figure made up of a rectangle and a circle connected by a long, thin rectangle. This configuration might represent various real-world objects, such as a lollipop, a simplified key, or certain types of tools or instruments. To find the total area of this figure, we would add the areas of the rectangle (l * w), the circle (πr²), and the connecting thin rectangle. The perimeter calculation would involve the circumference of the circle and the outer edges of the rectangles, excluding any parts where they connect. |
Applications of Polygons |

|
Math Clip Art--Geometry Concepts--Composite Figures--Composite Figure 9 |
Math Clip Art--Composite Figures--Composite Figure 9TopicGeometry Concepts DescriptionThis image shows a composite figure made up of a rectangle and a circle connected by a long, thin rectangle. This configuration might represent various real-world objects, such as a lollipop, a simplified key, or certain types of tools or instruments. To find the total area of this figure, we would add the areas of the rectangle (l * w), the circle (πr²), and the connecting thin rectangle. The perimeter calculation would involve the circumference of the circle and the outer edges of the rectangles, excluding any parts where they connect. |
Applications of Polygons |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 01 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 01TopicGeometry Concepts DescriptionThis image depicts a composite shape made up of a square and an equilateral triangle. This combination of shapes is commonly seen in architectural designs and various decorative patterns. To calculate the total area of this composite figure, we would add the area of the square (s²) to the area of the equilateral triangle (A = (√3/4)s², where s is the side length). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |
|
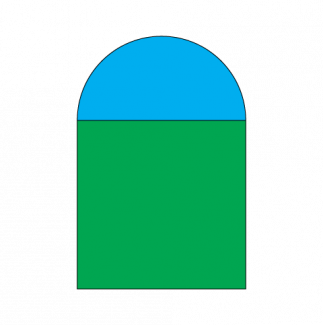
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 02 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 02TopicGeometry Concepts DescriptionThis image illustrates a composite shape made up of a square and a semicircle. This configuration is often seen in architectural elements such as arches and decorative motifs. To calculate the total area of this composite figure, we would add the area of the square (s²) to the area of the semicircle (½πr², where r is the radius of the semicircle). The perimeter would involve summing the lengths of the square's sides and the curved edge of the semicircle. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 03 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 03TopicGeometry Concepts DescriptionThis image shows a composite shape consisting of an equilateral triangle and a semicircle. This combination is often found in architectural designs and artistic patterns. To calculate the total area of this composite figure, we would add the area of the equilateral triangle (A = (√3/4)s²) to the area of the semicircle (½πr²). The perimeter would involve summing the lengths of the triangle's sides and the curved edge of the semicircle. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 04 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 04TopicGeometry Concepts DescriptionThis image depicts a composite shape made up of a regular hexagon and two equilateral triangles. This configuration is often seen in tessellation patterns and architectural designs. To calculate the total area of this composite figure, we would add the area of the hexagon (A = (3√3/2)s²) to the areas of the two equilateral triangles (A = (√3/4)s² for each). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 05 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 05TopicGeometry Concepts DescriptionThis image illustrates a "rocket ship" composite shape made up of a rectangle, two congruent right triangles, and an equilateral triangle. This playful configuration is often used in educational and design contexts to engage students. To calculate the total area of this composite figure, we would add the area of the rectangle (l * w), the areas of the two right triangles (½bh for each), and the area of the equilateral triangle (A = (√3/4)s²). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 06 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 06TopicGeometry Concepts DescriptionThis image shows a composite shape consisting of a regular hexagon with two semicircles. This configuration is often found in decorative patterns and architectural elements. To calculate the total area of this composite figure, we would add the area of the hexagon (A = (3√3/2)s²) to the areas of the two semicircles (½πr² for each). The perimeter would involve summing the lengths of the hexagon's sides and the curved edges of the semicircles. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 07 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 07TopicGeometry Concepts DescriptionThis image depicts a composite shape made up of a rectangle and two parallelograms. This configuration is often used in architectural designs and various structural layouts. To calculate the total area of this composite figure, we would add the area of the rectangle (l * w) to the areas of the two parallelograms (bh for each). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 08 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 08TopicGeometry Concepts DescriptionThis image illustrates a sawtooth composite shape made up of a rectangle and four congruent equilateral triangles. This configuration is often seen in mechanical designs and architectural elements. To calculate the total area of this composite figure, we would add the area of the rectangle (l * w) to the areas of the four equilateral triangles (A = (√3/4)s² for each). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 09 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 09TopicGeometry Concepts DescriptionThis image shows an hourglass composite shape made up of two congruent equilateral triangles, next to two congruent circular sectors. This configuration is often used in artistic designs and educational contexts. This design also has a shape that looks somewhat elliptical. To calculate the total area of this composite figure, we would add the areas of the two equilateral triangles (A = (√3/4)s² for each) to the areas of the two circular sectors (½r²θ for each, where θ is the central angle in radians). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Composite Figures--Simple Composite Shapes: 10 |
Math Clip Art--Composite Figures--Simple Composite Shapes: 10TopicGeometry Concepts DescriptionThis image depicts a composite shape made up of a rectangle, a parallelogram, and two congruent right triangles. This configuration is often used in architectural designs and various structural layouts. To calculate the total area of this composite figure, we would add the area of the rectangle (l * w), the area of the parallelogram (bh), and the areas of the two right triangles (½bh for each). The perimeter would involve summing the lengths of all outer sides, excluding any shared edges. |
Modeling Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 01 |
Math Clip Art--Roadside Geometry: 01TopicGeometry Concepts DescriptionThis image illustrates the "Do Not Enter" sign, which includes a circle and a square. A circle is a simple closed shape where all points are equidistant from the center. A square is a four-sided figure with congruent sides and four right angles. This sign has curved corners, but you can see the underlying geometry. Circles are used in road signs to convey clear, direct messages that need to be easily recognizable and universally understood. The symmetry and uniformity of a circle make it an effective shape for such signs. The same goes for square |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 02 |
Math Clip Art--Roadside Geometry: 02TopicGeometry Concepts DescriptionThis image depicts the "Stop" sign, which is an octagon. An octagon is an eight-sided polygon, and the regular octagon used for stop signs has equal sides and angles, with each interior angle measuring 135 degrees. The octagonal shape is unique and immediately recognizable, which is why it is used for stop signs. This distinct shape helps drivers quickly identify the sign and understand its message, enhancing road safety. Teacher's Script: "Look at the octagonal shape of the 'Stop' sign. Why do you think an octagon is used for stop signs? How does its unique shape help convey the message effectively?" |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 03 |
Math Clip Art--Roadside Geometry: 03TopicGeometry Concepts DescriptionThis image illustrates the "School Crossing" sign, which is typically a pentagon. A pentagon is a five-sided polygon, and the irregular pentagon used for school signs does not have equal sides and angles. A regular pentagon has five equal sides and angles, with each interior angle measuring 108 degrees. The pentagonal shape is used to denote school zones and crossings, providing a distinct and recognizable form that alerts drivers to the presence of children and the need for caution. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 04 |
Math Clip Art--Roadside Geometry: 04TopicGeometry Concepts DescriptionThis image depicts the "Yield" sign, which is a downward-pointing equilateral triangle. An equilateral triangle has three equal sides and angles, with each interior angle measuring 60 degrees. The triangular shape is used for yield signs to convey caution and alert drivers to give way to oncoming traffic. The distinct shape and orientation make it easily identifiable and effective in communicating the need to yield. Teacher's Script: "Look at the triangular shape of the 'Yield' sign. Why do you think a triangle is used for yield signs? How does its shape and orientation help convey the message effectively?" |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 05 |
Math Clip Art--Roadside Geometry: 05TopicGeometry Concepts DescriptionThis image illustrates the "County Road" sign, which is typically an irregular pentagon. A pentagon is a five-sided polygon. Teacher's Script: "Observe the pentagon shape of the 'County Road' sign. Why do you think pentagons are used for these types of signs? How does the shape help convey the message effectively?" For a complete collection of math clip art related to Geometry, click on this link: Math Clip Art: Geometry Concepts Collection. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 06 |
Math Clip Art--Roadside Geometry: 06TopicGeometry Concepts DescriptionThis image illustrates the "Railroad Crossing" sign, which is composed of two intersecting rectangles forming an X shape. Each rectangle has opposite sides that are equal and parallel, and all angles are right angles. The intersecting rectangles create a distinct X shape, which is used to denote railroad crossings. This configuration is easily recognizable and alerts drivers to the presence of train tracks, emphasizing caution and awareness. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 07 |
Math Clip Art--Roadside Geometry: 07TopicGeometry Concepts DescriptionThis image illustrates the "Bike Lane" sign, which is typically rectangular. A rectangle is a four-sided polygon with opposite sides that are equal and parallel, and four right angles. Rectangular signs are commonly used for informational purposes, providing clear and straightforward messages. The symmetry and simplicity of a rectangle make it a practical choice for road signs that convey directions or lane designations. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 08 |
Math Clip Art--Roadside Geometry: 08TopicGeometry Concepts DescriptionThis image depicts the "Road Closed" sign, which is typically rectangular. A rectangle is a four-sided polygon with opposite sides that are equal and parallel, and four right angles. Rectangular signs are commonly used for informational purposes, providing clear and straightforward messages. The symmetry and simplicity of a rectangle make it a practical choice for road signs that convey closures or restrictions. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 09 |
Math Clip Art--Roadside Geometry: 09TopicGeometry Concepts DescriptionThis image illustrates the "No Parking" sign, which is primarily rectangular in shape. A rectangle is a four-sided polygon with opposite sides that are equal and parallel, and four right angles. This rectangular shape serves as the main structure of the sign, providing a clear and straightforward format for conveying information. Inside the rectangle, there is a circular symbol, which is often used to emphasize regulatory messages. The circle, a simple closed shape where all points are equidistant from the center, draws attention to the specific prohibition or instruction, such as "No Parking." |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 10 |
Math Clip Art--Roadside Geometry: 10TopicGeometry Concepts DescriptionThis image depicts the "No U-Turn" road sign, which is primarily square in shape. A square is a four-sided polygon with equal sides and angles, providing a symmetrical form that is easily recognizable. Inside the square is a circular section that displays the prohibition of making a U-turn, highlighting the specific action being regulated. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 11 |
Math Clip Art--Roadside Geometry: 11TopicGeometry Concepts DescriptionThis image illustrates the "Railroad Crossing" sign, which is circular. A circle is a simple closed shape where all points are equidistant from the center. Circular signs are often used for regulatory purposes, drawing attention due to their distinct shape. The interior of the sign shows an X, which highlights the railorad crossing. Another variation of this sign is the X-shaped version. Circles are used in road signs to convey clear, direct messages that need to be easily recognizable and universally understood. The symmetry and uniformity of a circle make it an effective shape for such signs. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 12 |
Math Clip Art--Roadside Geometry: 12TopicGeometry Concepts DescriptionThis image depicts the "Road Work" sign, which is typically diamond-shaped. A diamond shape, or rhombus, is a four-sided polygon with equal sides and opposite equal angles. Diamond-shaped signs are used to convey warnings and cautionary messages. The distinct shape draws attention and helps drivers quickly recognize the need for caution due to road work or other temporary conditions. Teacher's Script: "Look at the diamond shape of the 'Road Work' sign. Why do you think diamond shapes are used for warning signs? How does the shape help convey the message effectively?" |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 13 |
Math Clip Art--Roadside Geometry: 13TopicGeometry Concepts DescriptionThis image illustrates the "Speed Limit" sign, which is typically rectangular. A rectangle is a four-sided polygon with opposite sides that are equal and parallel, and four right angles. Rectangular signs are commonly used for informational purposes, providing clear and straightforward messages. The symmetry and simplicity of a rectangle make it a practical choice for road signs that convey speed limits or other regulatory information. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 14 |
Math Clip Art--Roadside Geometry: 14TopicGeometry Concepts DescriptionThis image depicts the "No Passing Zone" sign, which is typically a pennant-shaped isosceles triangle. This triangle has two equal sides and a distinct pointed shape that indicates caution. The pennant shape is used to signal no passing zones, providing a clear and recognizable warning to drivers. Its unique orientation and shape help convey the message effectively, alerting drivers to maintain their lane. |
Identifying Shapes |

|
Math Clip Art--Geometry Concepts--Roadside Geometry: 15 |
Math Clip Art--Roadside Geometry: 15TopicGeometry Concepts DescriptionThis image illustrates the "Street Light" sign, which is typically rectangular. A rectangle is a four-sided polygon with opposite sides that are equal and parallel, and four right angles. In this case the rectangle is rotated to look like a diamond shape. Rectangular signs are commonly used for informational purposes, providing clear and straightforward messages. The symmetry and simplicity of a rectangle make it a practical choice for road signs that convey information about street lighting or other amenities. |
Identifying Shapes |

|
Video Transcript: Geometry Applications: Polygons |
Video Transcript: Geometry Applications: Polygons
This is the transcript for the video of same title. Video contents: In this program we explore the properties of polygons. We do this in the context of two real-world applications. In the first, we look at Islamic tile patterns as examples of regular polygons. We explore how such intricate patterns were created using a compass and straight edge. In the second application we look at composite figures, specifically in the context of the design of the Petronas Towers in Indonesia. |
Applications of Polygons |

|
Video Transcript: Geometry Applications: Polygons, Segment 1: Introduction |
Video Transcript: Geometry Applications: Polygons, Segment 1: Introduction
This is the transcript for the video of same title. Video contents: The Pentagon is one of the most famous polygon-shaped buildings in the world. But why was this shape chosen over a more straightforward quadrilateral shape? We briefly explore the properties of pentagons and use this as a way of introducing the key concepts throughout the program. |
Applications of Polygons |

|
Video Transcript: Geometry Applications: Polygons, Segment 2: Properties of Polygons |
Video Transcript: Geometry Applications: Polygons, Segment 2: Properties of Polygons
This is the transcript for the video of same title. Video contents: In the ancient city of Marrakesh polygons are on display. As part of the Islamic tile work prevalent throughout the Middle Ages, Marrakesh provides an opportunity to explore the properties of polygons, and how these properties are taken advantage of in the intricate designs found throughout this fascinating city. |
Applications of Polygons |

|
Video Transcript: Geometry Applications: Polygons, Segment 3: Composite Figures |
Video Transcript: Geometry Applications: Polygons, Segment 3: Composite Figures This is the transcript for the video of same title. Video contents: The Petronas Towers in Indonesia provide an opportunity to explore the composite shapes used in the design of the towers. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link.Note: The download is a PDF file.Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Polygons |

|
Video Transcript: Geometry Applications: Polygons, Segment 3: Composite Figures |
Video Transcript: Geometry Applications: Polygons, Segment 3: Composite Figures This is the transcript for the video of same title. Video contents: The Petronas Towers in Indonesia provide an opportunity to explore the composite shapes used in the design of the towers. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link.Note: The download is a PDF file.Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Polygons |